Intro
몇 가지 문제로 시작해 보겠습니다.
Mazes at Hever Castle, UK
영국은 유구한 역사를 지닌 나라답게 웅장한 크기를 자랑하는 castle과 오래된 건축물을 쉽게 찾아볼 수 있습니다. 사진은 영국 Hever Castle과 내부에 있는 미로입니다. 미로는 입구에서 출발하여 출구로 나가는 길을 찾아야 합니다. 갈림길이 나오면 어떤 길로 갈 것인지 선택하고, 막다른 길을 만나면 되돌아가야 합니다. 이것은 미로 문제입니다.
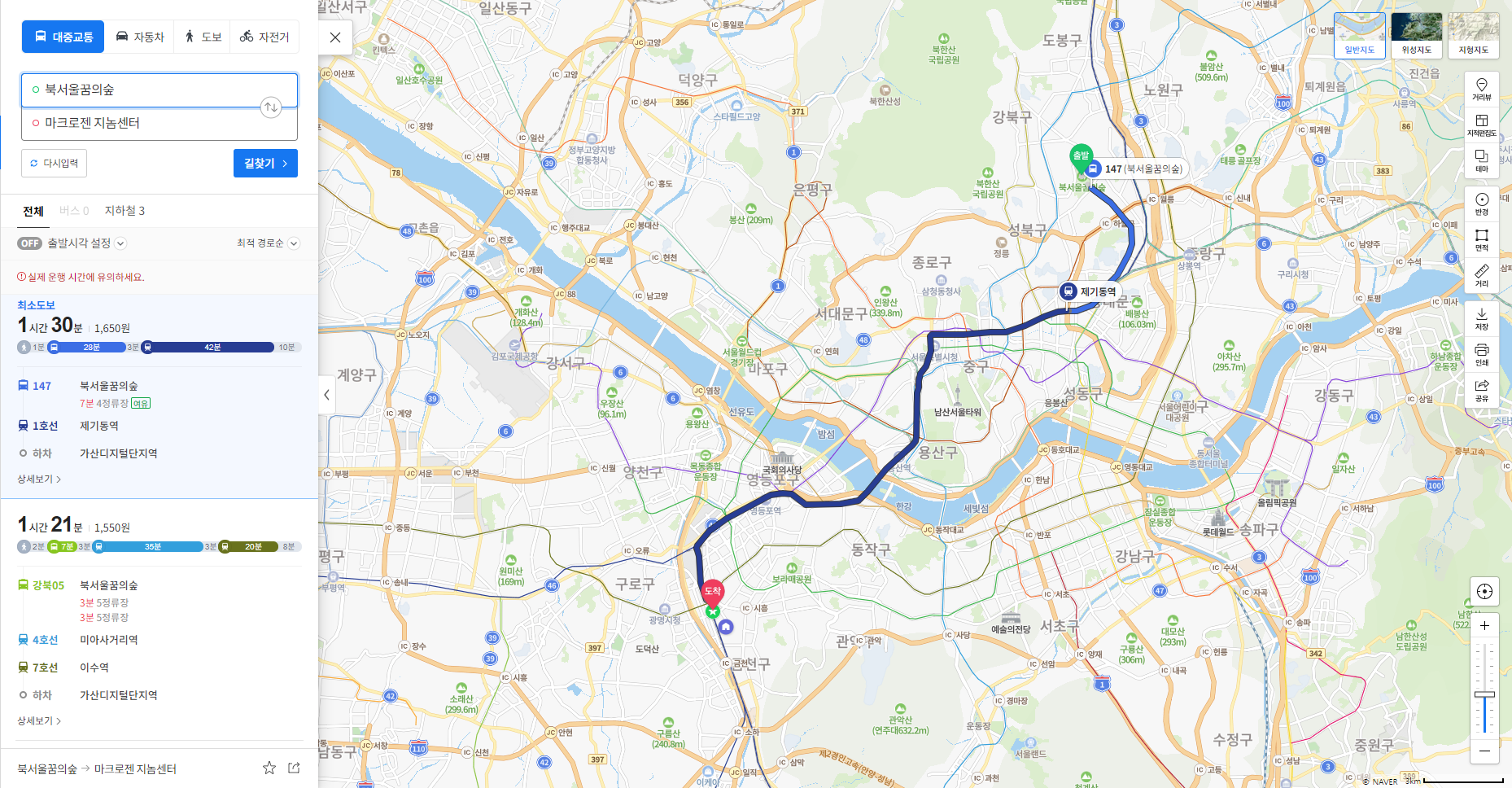
Hubert’s commute path
매일 오고가는 출퇴근 경로입니다. 1.5시간이 소요되는 버스+지하철 조합을 이용합니다. 우리는 목적지까지 도달하는데 버스, 지하철, 택시, 자가용 등 다양한 교통수단을 사용할 수 있고 직통, 환승 등 조합에 따라 소요 시간은 천차만별 입니다. 대부분 가장 빠른 경로를 원하겠지요? 이것은 최적경로 찾기 문제입니다.
미로 문제와 최적경로 찾기 문제, 어떻게 논리적으로 해결할 수 있을까요?
Algorithm: Search
Search algorithm으로 문제를 해결할 수 있습니다. 연속 변수나 이산 변수를 사용하여 일부 데이터 구조 안에 저장된 정보를 search하는 algorithm입니다.
Search algorithm 구성 요소는 다음과 같습니다.
Agent: 주변 환경을 인식하고 상호작용하는 주체입니다.
State: 환경 내에서 agent가 배치된 모양입니다. Agent가 action을 시작하기 전 초기 위치를 initial state라고 합니다.
Actions: 특정 환경 안에서 문제가 주어졌을 때 agent가 선택 가능한 행동들을 의미합니다. ACTIONS(s)는 state s에서 실행가능한 모든 action을 반환합니다.
Transition model: 특정 state에서 가능한 action을 취한 결과 나타나는 states를 설명하는 model입니다. RESULT(s, a)는 state s에서 action a를 수행한 result state를 반환합니다.
Simulation: Agent는 곧바로 action을 취하지 않습니다. 사전에 어떤 action이 가장 효율적인지 model을 사용하여 simulation을 진행합니다.
Goal test: action 결과로 얻은 state가 처음 목표로 했던 state인지 평가하는 것입니다.
Path cost function: Path를 따라 goal state에 도달하기 까지 소요된 비용을 산출하는 함수입니다.
Solution: Simulation을 통해 얻은 일종의 정답입니다. 다양한 solution 중 가장 비용이 적게 드는 것을 Optimal Solution이라고 합니다.
DFS (Deep-First Search)
DFS (Deep-First Search)는 search algorithm 종류 중 하나입니다. Goal test를 만족할 때까지 가장 깊은 단계 node까지 확장하며 search하는 방식입니다. DFS가 작동하는 process를 살펴보면 이해가 쉽습니다.
DFS는 stack structure를 사용하여 아래 process에 따라 진행합니다. Frontier와 explored set이 존재합니다. Frontier는 initial state(A)를 포함한 state입니다. Explored set는 empty state로 시작합니다. Process가 종료될 때까지 반복합니다.
Frontier에 search할 next node 확인: Frontier에 search할 next node가 존재하는지 확인합니다. 만약 없다면 solution이 없음을 의미하며 DFS process를 종료합니다. 참고로 여기서 언급한 node는 state, parent node, action, path cost 정보를 담고 있는 data structure입니다.
Next node 가져오기: Frontier에서 last node를 추출합니다. (stack structure)
Solution 확인과 return: 2번의 node가 goal test를 통과하면 search process를 종료하고 explored set을 solution으로 정의한 뒤 return합니다.
Explored set에 node 추가: 2번의 node가 goal test를 통과하지 못하면 explored set에 node를 추가합니다.
Frontier expansion: Frontier에 child node를 추가 합니다. 이 때 child node가 frontier와 explore set에 이미 존재하는지 확인합니다.
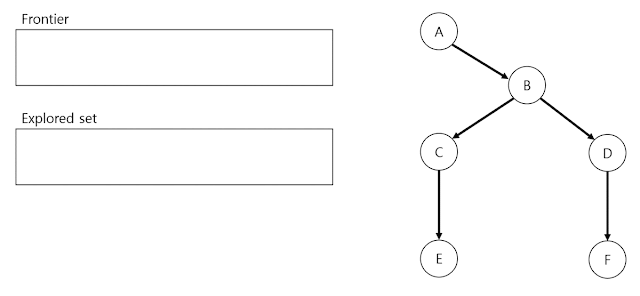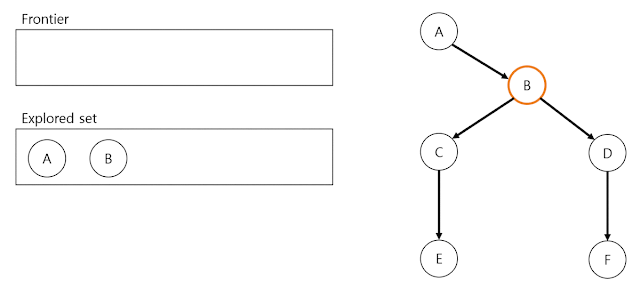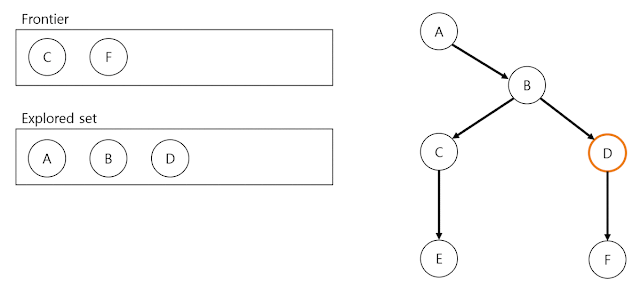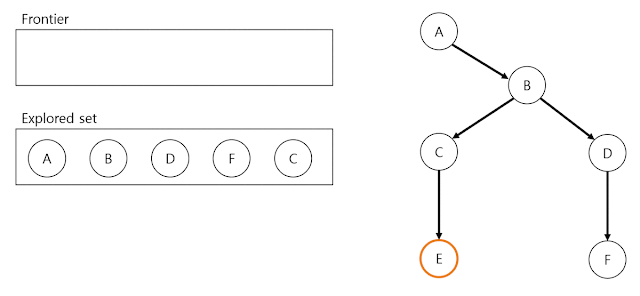DFS process
위 예시 과정에서 goal state는 node(E)입니다. DFS process에서 last node(F)에 다다르면 goal state인 node(E)와 일치하는지 확인합니다. 일치하지 않으므로 마지막 분기 node(B)로 돌아가서 같은 방식으로 process를 이어갑니다. 다시 last node(E)에 다다르면 goal state인 node(E)와 비교하고 일치하므로 explored set을 solution으로 return하고 DFS process를 종료합니다.
DFS 공간 복잡도, 시간 복잡도
Node의 수를 V(Vertex), 연결선의 수를 E(Edge)라고 할 때,
DFS의 공간 복잡도는 다음과 같습니다.
인접 행렬인 경우: O($V^2$)
인접 리스트인 경우: O(V+E)
시간 복잡도는 다음과 같습니다.
인접 행렬인 경우: O($V^2$)
인접 리스트인 경우: O(V+E)
DFS 장/단점
DFS의 장점은 다음과 같습니다.
BFS(Breath-First Search)보다 작은 저장공간이 필요합니다. 지나간 모든 node를 저장할 필요 없이 분기점의 node들만 저장합니다.
Goal state인 node가 깊은 단계에 존재할수록 BFS보다 빠릅니다.
DFS의 단점은 다음과 같습니다.
Goal state인 node가 아닌 다른 last node들의 깊이가 깊을수록 많은 시간을 소비합니다.
항상 optimal solution을 찾는 것은 아닙니다. DFS는 goal state인 node를 만나는 순간 종료되기 때문입니다.
DFS 적용
DFS를 미로 문제에 적용해 보겠습니다.
Node class는 node 객체를 생성합니다. Node는 앞서 언급한 것처럼 agent state, parent node, 그리고 action에 대한 정보를 가지고 있습니다.
DFS는 stack structure를 사용하여 node를 search 합니다.
Maze() class: 미로 문제가 담긴 파일을 읽습니다. 시작 위치(S), 종료 위치(E), 벽, 그리고 길을 파악하여 row * column 크기의 행렬로 정리합니다.
StackFrontier() class: 비어있는 list 형태의 frontier 객체를 생성 합니다.
print_out function: 미로와 solution을 출력합니다.
neighbors function: 현재 node에서 이동 가능한 node로의 방향과 좌표를 확인하고 모두 return 합니다.
solve function: Solution을 발견하거나 더 이상 frontier에 search할 node가 남아있지 않을 때까지 search 과정을 반복 수행합니다.
output_image function: 미로와 발견한 solution을 image 파일로 출력합니다.
add function: Frontier에 다음 단계 child node를 추가 합니다.
contains_state function: Node가 이미 frontier에 들어 있는지 search 합니다.
empty function: Frontier에 담긴 node count가 0인지 확인 합니다. Frontier에 더 이상 가져올 node가 없는지 확인하는 function 입니다.
remove function (116 line): 본 class의 핵심 function 입니다. DFS는 stack structure를 사용하므로 가장 마지막 위치의 node를 가져옵니다.
DFS 예제
미로 문제를 입력받아 solution을 찾아내는 과정입니다. 전체 code와 예제 파일은 이 곳에서 확인할 수 있습니다.
DFS 미로 문제 예제
하지만 앞서 언급한 것처럼 DFS의 단점 중 하나는 항상 optimal solution을 찾는 것이 아니라는 것입니다. 위 예제 화면에서도 가까운 길을 두고 먼 길을 돌아 찾아 갔습니다. 이런 경우 optimal solution을 어떻게 찾을 수 있을까요? 바로 BFS(Breath-First Search)를 사용하는 것입니다.