본 post는 국가생명연구자원정보센터(KOBIC) 주관 경희대학교 이과대학 김권일 교수님의 딥러닝 알고리즘 2를 정리한 내용입니다.
Intro
Machine learning 관련 기초 개념을 확인하고, 공개된 논문내용 및 데이터를 바탕으로 직접 실습하고 학습하는 과정입니다.
오차 역전파 알고리즘
최적의 학습 결과를 갖는 neural network를 설계하려면 근본적으로 입력이나 특정 neuron의 weight를 약간 변경시키면 출력에 작은 변화가 일어난다는 점에 근거하고 있습니다. 여기서 activation function으로 쓰이는 sigmoid function은 0에서 1까지 연속적으로 변하는 출력을 갖기 때문에 weight나 bias를 조금 변화시켰을 때 출력이 조금씩 변하도록 만들 수 있습니다.
Neural network는 backpropagation(역전파)를 통해 “역방향으로 error를 전파”시키면서 최적의 학습 결과를 찾아가는 것이 가능합니다. Backpropagation을 수행하기 위해 사용되는 cost function(loss function)은 다음과 같이 정의됩니다.
\[C(w, b) \equiv \frac{1}{2n} \sum_{x}^{} ||y(x) - a||^2\]n은 training에 사용되는 input node의 수
y(x)는 입력 x를 넣었을 때 기대 출력
a는 실제 출력
을 의미합니다. 이를 mean square error (MSE; 평균제곱 오차)라고 부르며, 학습의 최종 목표는 MSE를 최소화하는 것입니다. Cost function에서 예측 값과 label의 오차를 절대값이 아닌 제곱으로 처리하는 이유는 다음과 같습니다.
오차가 큰 경우에 더 큰 가중치를 주어 학습을 빠르게 처리합니다.
MSE를 볼록함수(convex function)로 만들어 최적의 weight를 효과적으로 찾기 위함입니다.
절대값은 미분불가능 수식이기 때문입니다.
Gradient descent(경사 하강법)을 기반으로 backpropagation을 진행하며 학습을 수행합니다.
MSE와 Gradient Descent
MSE를 최소로 만드는 w와 b의 해를 찾는 방법입니다. 우선 b를 무시하고 w에 집중해보면, MSE는 w를 중심으로 한 convex function(볼록 함수)입니다. 아래로 볼록한 convex function이며 이 함수의 최소값을 찾는 것, 즉 error를 최소화하는 값을 찾는 과정입니다.
일단 w를 1로 설정합니다.
w=1에서의 접선의 기울기를 계산하면, 최소값으로 가기 위한 방향과 크기를 찾을 수 있습니다.
접선의 방향이 양수가 나온다는 것은 MSE가 양의 방향으로 증가하는 경향을 보인다는 의미합니다.
증가하면 안되니 반대방향으로 가야합니다.
접선 만큼의 크기를 원래 w에서 빼주면 최소값으로 갈 수 있습니다.
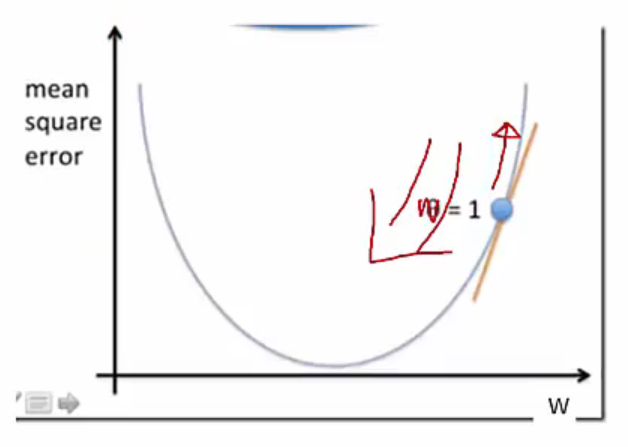Gradient Descent
https://www.edwith.org/deep-learning-2023/lecture/1475086
Gradient Descent를 위한 편미분
Neural network 크기가 커지고 입력이나 출력의 개수가 많아지면 parameter의 수가 너무 많기 때문에 weight와 bias를 조절하여 cost function을 최소화하는 작업이 매우 어렵게 됩니다.
입력이나 출력의 개수가 많아진 상태에서 weight나 bias 값을 작게 변화시키면, 출력 쪽에서 생기는 변화 역시 매우 작게 생기며, 작은 구간만 놓고 보았을 때 선형적인 관계가 있습니다. 작은 변화의 관점에서는 선형적인 관계이기 때문에, 출력에서 생긴 오차를 반대의 입력 쪽으로 전파시키면서 weight와 bias 등을 갱신합니다.
Cost function이 weight와 bias의 함수로 이루어졌기 때문에 출력 부분부터 시작해서 입력 쪽으로(역방향으로) 순차적으로 cost function에 대한 편미분을 구하고 여기에서 얻은 편미분 값을 이용하여 weight와 bias 값을 갱신합니다.
모든 training data에 대해 이 작업을 반복적으로 수행하다 보면, training data에 최적화된 weight와 bias 값들을 얻을 수 있습니다. Backpropagation은 출력부터 반대 방향으로 순차적으로 편미분을 수행해 나가면서 weight와 bias 값들을 갱신시킨다는 의미입니다.
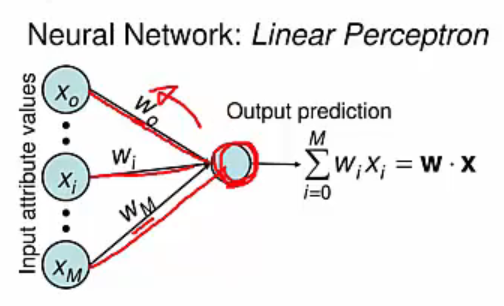Neural Network에서의 편미분
https://www.edwith.org/deep-learning-2023/lecture/1475086
Backpropagation 상세: Chain Rule
Chain rule을 이용하면 backpropagation 식을 좀 더 쉽게 풀어낼 수 있습니다. 여기서 chain rule이란, 합성함수 y=f(g(x))가 t=g(x), y=f(t)로 분해될 때 다음이 성립함을 나타내는 법칙입니다.
\(\frac{dy}{dx} = \frac{dy}{dt} \frac{dt}{dx}\)
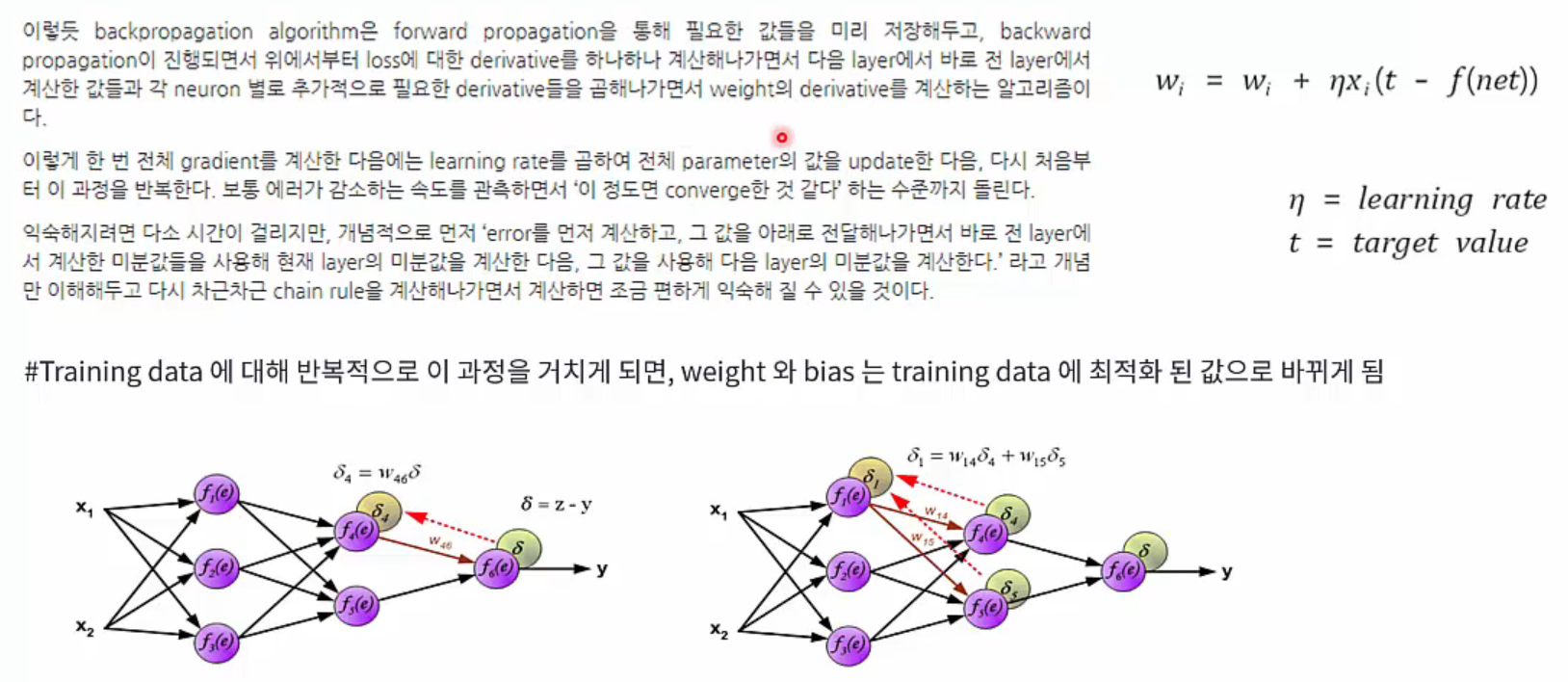Backpropagation
https://www.edwith.org/deep-learning-2023/lecture/1475086
Backpropagation 장단점
Hornik et al, 1989의 연구에서 hidden node가 충분히 많다면 activation function으로 무엇을 사용하든 multi-layer feedforward neural network는 어떤 함수라도 원하는 정확도만큼 슨사화할 수 있음을 증명했습니다. 그러나 hidden layer의 neuron 개수를 어떻게 설정하느냐는 아직도 해결되지 않은 문제이며, 시행착오 방법에만 의존해서 조정할 수 밖에 없습니다.
Backpropagation neural network는 강력한 능력으로 인해 overfitting 현상을 자주 겪게 됩니다. 두 가지 전략을 통해 overfitting을 완화시킬 수 있습니다.
Early stopping(조기 종료): Data를 training set과 validation set으로 분리합니다. Training set은 gradient descent를 계산하고 weight와 bias를 갱신하는데 사용합니다. Validation set는 error를 예측하는데 사용되고 만약 training set의 error가 줄어들 때 validation set의 error가 높아진다면 즉시 훈련을 종료하는 방법입니다.
Regularization(정규화): Cost function에 weight와 bias의 제곱합과 같은 network 복잡도를 표현하는 부분을 추가하는 방법입니다.
Deep Learning
이론상으로 parameter 수가 많으면 많을수록 model의 복잡성이 높아지고 예측 및 분류 능력이 커집니다. 이는 아무리 복잡한 학습 문제라도 parameter를 증가시키면 해결이 가능하다는 것을 의미합니다. 그러나 동시에 복잡한 model의 훈련 효과가 좋지 않고 쉽게 overfitting에 빠집니다.
최근 클라우드 컴퓨터와 빅데이터 시대가 도래하면서 컴퓨터의 능력은 대대적으로 높아졌고 훈련 성능 저하 문제를 완화시켰습니다. 그리고 training data가 많아짐에 따라 overfitting 위험은 대폭 낮아졌습니다. 이에 따라 deep learning을 대표로 하는 복잡한 model들이 사람들의 관심을 받기 시작했습니다. 전형적인 deep learning model은 깊은 층을 쌓은 neural network입니다. Neural network model의 능력을 향상시킬 수 있는 가장 간단한 방법은 hidden layer 개수를 늘리는 것입니다.
Hidden layer가 많으면 상응하는 neuron 연결 weight, 임계값 등의 parameter 수가 늘어납니다. Model의 복잡성도 단순히 hidden layer neuron 수를 증가시키는 것만으로 늘릴 수 있습니다. 하지만 model의 복잡성을 증가시키는 관점에서 바라보면 hidden layer의 개수를 증가시키는 것이 hidden layer neuron의 수를 증가시키는 것보다 효율적입니다. Hidden layer의 수를 증가시키면 activation function을 가진 neuron의 개수를 늘리게 될 뿐 아니라 activation function이 내장된 층 수도 증가하기 때문입니다.
그러나 여러 hidden layer를 가진 neural network는 전통적인 algorithm(backpropagation)을 사용하여 훈련시키기 힘든 점이 있습니다. 오차가 hidden layer에서 backpropagation 될 때 vanishing(소실)되어 update 하기 어려운 점이 있기 때문입니다. 이러한 현상을 vanishing gradient라고 합니다.
Global Minimum and Local Minimum
만약 E로 neural network의 training set에 대한 error를 나타낸다면, 이는 weight와 bias(threshold)에 관한 함수일 것입니다. 이 때 neural network의 훈련 과정은 하나의 parameter 탐색 과정이라고 볼 수 있습니다. 즉, parameter 공간에서 최적의 parameter를 찾아 E를 최소화 하는 것입니다. 여기에는 두 가지 종류의 ‘최적’이 있습니다. 바로 local minimum과 global minimum입니다.
Local minimum은 parameter 공간의 어떤 점이 되고 주변 점들의 cost function(loss function, error 함수값)이 해당 점의 함수값보다 작으면 안됩니다. 이와 비슷하게 global minimum의 해는 parameter 공간 내의 모든 점들이 error 함수값보다 작지 않다는 것을 의미합니다.
Gradient descent 방법은 임의의 시작점에서 출발해 반복적으로 최적의 parameter 값을 찾아 나갑니다. 매번 반복할 때마다 우리는 먼저 cost function이 해당 점에서 갖는 기울기를 계산하고 그 기울기에 따라 탐색 방향을 정합니다. 만약 해당 점에서 cost function의 기울기가 0이라면 이미 local minimum에 도달한 것입니다. 이는 parameter 반복 갱신이 그 점에서 멈출 것이라는 의미입니다. 또한 cost function이 하나의 local minimum만을 갖는다면 해당 값이 바로 global minimum이 됩니다.
Local Minimum 함정 탈출 전략
https://www.edwith.org/deep-learning-2023/lecture/1475086
Take Home Message
Summary 1
https://www.edwith.org/deep-learning-2023/lecture/1475086
Summary 2
https://www.edwith.org/deep-learning-2023/lecture/1475086