파이썬을 활용한 데이터 분석 (중급) - 1. One Sample t-Test with python

본 post는 국가생명연구자원정보센터(KOBIC) 주관 인사이트마이닝 이부일 CEO의 One Sample t-Test with Python을 정리한 내용입니다.

Intro

---

Python을 이용하여 One sample t-test 수행과정을 알아봅니다.

언제 사용하는가?

---

One sample t-test는 하나의 모집단의 평균이 기존보다 커졌는지, 작아졌는지, 같지 않은지를 분석할 때 사용합니다. 데이터는 수치형 자료를 사용합니다.

가설 세우기

---

• 귀무가설 (Null Hypothesis, H₀)
  • 모집단의 평균은 \(\mu\)₀입니다. (\(\mu\) = \(\mu\)₀)
• 대립가설 (Alternative Hypothesis, H₁ or H_A)
  • 연구자가 지지하는 가설입니다. (채택되길 바라는 가설)
  • 모집단의 평균은 \(\mu\)₀보다 큽니다. (\(\mu > \mu\)₀)
  • 모집단의 평균은 \(\mu\)₀보다 작습니다. (\(\mu < \mu\)₀)
  • 모집단의 평균은 \(\mu\)₀와 같지 않습니다. (\(\mu \neq \mu\)₀)
    
    

유의수준 (Significant Level, \(\alpha\))

---

표본에서 관찰된 검정통계량이 어떤 값이 나오는지에 따라 귀무가설로 결론을 내릴지, 아니면 대립가설로 결론을 내릴지 결정하는 기준입니다. 보통 0.05로 설정합니다.

유의확률 (Significanct Probability)

---

표본에서 관찰된 검정통계량이 귀무가설이 맞다는 가정 하에서 얼마나 일어날까 알려주는 값입니다.

• 유의확률 < 유의수준 : 대립가설
  • 표본에서 관찰된 값이 귀무가설이 맞다는 가정 하에서 일어나기 어려운 사건인데 일어난 상태입니다.
  • 대립가설을 지지합니다.
• 유의확률 >= 유의수준 : 귀무가설
  • 표본에서 관찰된 값이 귀무가설이 맞다는 가정 하에서 일어나기 쉬운 사건인데 일어난 상태입니다.
  • 귀무가설을 지지합니다.
    
    

검정통계량 (Test Statistics)

---

• \[t = \frac{\bar y - \mu_{0}}{s/\sqrt n}\]
• t(n-1) 분포를 따릅니다.
• (n-1)은 자유도(df, degree of freedom) 입니다.
  
  

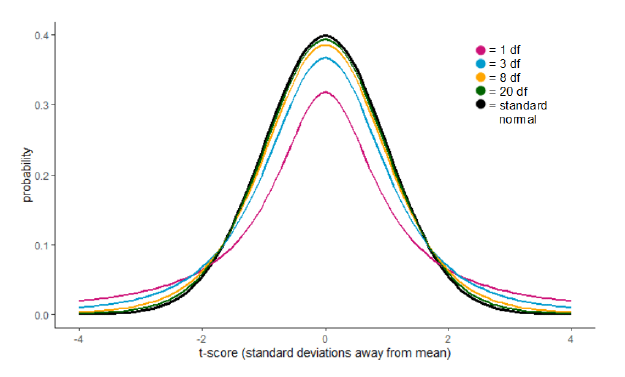t-Test
https://www.edwith.org/python-data-analysis-2023/lecture/1475043

실습

---

• 가설 설정
  • 귀무가설: 환자들의 평균 키는 15인치 입니다.
  • 대립가설: 환자들의 평균 키는 15인치와 같지 않습니다.
    
    

가설 설정
https://www.edwith.org/python-data-analysis-2023/lecture/1475043

• 분석 1단계: 정규성 검정(Normality Test)
  • 귀무가설: 정규분포를 따릅니다. (정규분포를 따라야만 One sample t-test를 수행할 수 있습니다.)
  • 대립가설: 정규분포를 따르지 않습니다.
  • n < 5,000 : Shapito-Wilk Normality Test (shapiro(data.variable))
  • n >= 5,000 : Anderson-Darling Normality Test (anderson(data.variable))
  • shapiro normality test의 유의확률(p-value)가 0.79로 귀무가설(정규분포 따름)을 만족합니다.
    
    

정규성 검정
https://www.edwith.org/python-data-analysis-2023/lecture/1475043

• 분석 2단계: One sample t-test
  
  

정규성 검정
https://www.edwith.org/python-data-analysis-2023/lecture/1475043

* patient.height: 검정변수
* popmean: 귀무가설이 참일 때 모평균
* alternative: 대립가설 -> 'greater' or 'less' or 'two-sided'
* One sample t-test의 유의확률(p-value)가 0.120으로 유의수준인 0.05보다 큽니다. 즉, 환자들의 평균 키는 15인치라는 귀무가설을 지지합니다. <br><br>

코드

---

import pandas as pd
import scipy.stats as stats
from scipy.stats import shapiro, anderson

# load data
patient = pd.read_excel(
    io='01patient.xlsx',
    sheet_name=0
    )
print(patient)

# Analysis I: Normality Test
# n < 5,000 -> Shapito-Wilk Normality Test
shapiro_test = shapiro(patient.height)
print(shapiro_test)

# Analysis II: One sample t-test
stats.ttest_1samp(
    patient.height,
    popmean = 15,
    alternative = 'two-sided'
)

Take Home Message

---

One sample t-Test 이론을 학습하고 Google colab에서 실습해 보았습니다.