파이썬을 활용한 데이터 분석 (중급) - 3. Two Sample t-Test with python

본 post는 국가생명연구자원정보센터(KOBIC) 주관 인사이트마이닝 이부일 CEO의 Two Sample t-Test with python을 정리한 내용입니다.

Intro

---

Python을 이용하여 Two Sample t-Test with python 수행과정을 알아봅니다.

언제 사용하는가?

---

Two Sample t-Test는 두 개의 독립적인 모집단의 평균이 같은지, 다른지, 같지 않은지를 분석하는 방법입니다. 두 개이 모집단이 모두 정규성 가정을 만족할 때 사용합니다.

가설 세우기

---

• 귀무가설 (Null Hypothesis, H₀)
  • 수면제품(A, B)에 따라 수면시간에 차이가 없습니다.
• 대립가설 (Alternative Hypothesis, H₁ or H_A)
  • 수면제품(A, B)에 따라 수면시간에 차이가 있습니다.
    
    

Two Sample t-Test

---

• 1단계: 정규성 검정(Normality Test)
  • 귀무가설: 정규분포를 따릅니다.
  • 대립가설: 정규분포를 따르지 않습니다.
  • n < 5,000: Shapiro-Wilk Normality Test
  • n >= 5,000: Anderson-Darling Normality Test
• 2단계: 등분산 검정(F-test of Equality of Variances)
  • 귀무가설: 등분산입니다.
  • 대립가설: 이분산입니다.
• 3단계-1: Two Sample t-Test (등분산)
  • 등분산이 가정된 Two Sample t-Test를 계산합니다.
  • \(t = frac{(\bar x_{1} - \bar x_{2}) - (\mu_{1} - \mu_{2})}{S_{p}\sqrt(\frac{1}{n_{1}}-\frac{1}{n_{2}})}\)
    
    

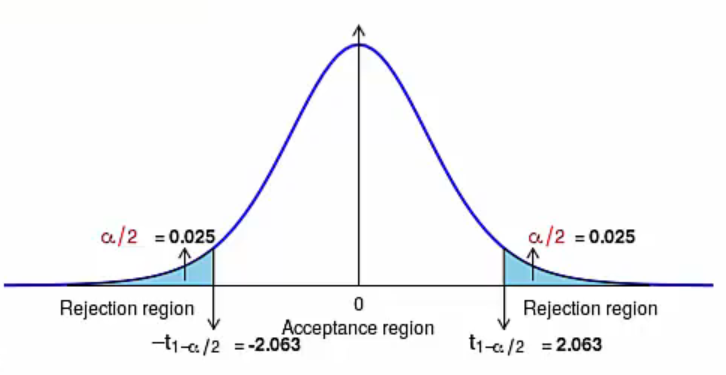t분포
https://www.edwith.org/python-data-analysis-2023/lecture/1475045

• 3단계-2: Two sample t-test (이분산)
  • 이분산이 가정된 Two Sample t-Test를 계산합니다.
  • \[t = frac{(\bar x_{1} - \bar x_{2}) - (\mu_{1} - \mu_{2})}{\sqrt(\frac{S_{1}^{2}}{n_{1}}+\frac{S_{2}^{2}}{n_{2}})}\]
  • 등분산과 마찬가지로 t분포를 따릅니다.
    
    

실습

---

• 가설 설정
  • 귀무가설: 수면제품(A, B)에 따라 수면시간에 차이가 없습니다.
  • 대립가설: 수면제품(A, B)에 따라 수면시간에 차이가 있습니다.
    
    

데이터 로딩
https://www.edwith.org/python-data-analysis-2023/lecture/1475045

• 분석 1단계: 정규성 검정(Normality Test)
  • 귀무가설: 정규분포를 따릅니다.
  • 대립가설: 정규분포를 따르지 않습니다.
  • n < 5,000 : Shapito-Wilk Normality Test (shapiro(data.variable))
  • n >= 5,000 : Anderson-Darling Normality Test (anderson(data.variable))
  • shapiro normality test 결과 A 그룹의 유의확률(p-value)가 0.408, B 그룹의 유의확률(p-value)가 0.351로 귀무가설(정규분포 따름)을 만족합니다.
    
    

정규성 검정
https://www.edwith.org/python-data-analysis-2023/lecture/1475045

• 분석 2단계: 등분산 검정(F-test of Equality of Variances)
  • 귀무가설: 등분산입니다.
  • 대립가설: 이분산입니다.
    
    

등분산 검정
https://www.edwith.org/python-data-analysis-2023/lecture/1475045

• 분석 3단계: 등분산이 가정된 Two Sample t-Test
  • 등분산이 가정된 Two Sample t-Test 분석결과 유의확률(p-value)가 0.079로 귀무가설을 만족합니다. 즉, 수면제품(A, B)에 따라 수면시간에 차이가 없습니다.
    
    

등분산이 가정된 Two Sample t-Test
https://www.edwith.org/python-data-analysis-2023/lecture/1475045

코드

---

import pandas as pd
import seaborn as sns
import scipy.stats as stats
from scipy.stats import shapiro

# load data
sleep = pd.read_excel(
    io = '03sleep.xlsx',
    sheet_name = 0
)
print(sleep)


# Analysis I: Normality Test
# n < 5,000 -> Shapito-Wilk Normality Test
# group A
shapiro_test_A = shapiro(sleep.loc[sleep["product"] == "A", "time"])
print(shapiro_test_A)

# 유의확률(0.408) > 유의수준(0.05)) : 귀무가설 -> 정규성 가정을 만족합니다.


# group B
shapiro_test_B = shapiro(sleep.loc[sleep["product"] == "B", "time"])
print(shapiro_test_B)

# 유의확률(0.351) > 유의수준(0.05)) : 귀무가설 -> 정규성 가정을 만족합니다.


# Analysis II: 등분산(성) 검정
stats.levene(
    sleep.loc[sleep["product"] == "A", "time"],
    sleep.loc[sleep["product"] == "B", "time"]
)

# 유의확률(0.624) > 유의수준(0.05) : 귀무가설 -> 등분산을 만족합니다.


# Analysis III: 등분산이 가정된 Two sample t-test
stats.ttest_ind(
    sleep.loc[sleep["product"] == "A", "time"],
    sleep.loc[sleep["product"] == "B", "time"],
    equal_var = True,
    alternative = 'two-sided'
)

# 유의확률(0.079) > 유의수준(0.05) : 귀무가설 -> 수면제(A, B)에 따라 수면시간에 통계적으로 유의한 차이는 없습니다.

Take Home Message

---

Two Sample t-Test 이론을 학습하고 Google colab에서 실습해 보았습니다.