Intro
확률의 naive한 정의로 접근하기 어려운 경우를 알아내고, story proof를 통한 접근을 학습합니다. 또한 확률의 non-naive한 정의를 위한 공리 2가지를 이해하고 적용할 수 있습니다.
Tips for Solving Problems
| (header) | order matter | order doesn’t matter |
| replace | $n^{k}$ | $\binom{n+k-1}{k}$ |
| doesn’t replace | n(n-1)(n-2)…(n-k+1) | $\binom{n}{k}$ |
Sampling table에서 대부분 multiplication rule에 따라 설명되지만, ‘replace-order doesn’t matter’인 경우 그렇지 않습니다.
정답을 확인할 때 다음과 같은 방법을 사용할 수 있습니다.
- Labeling: Data에 사람, 구슬 등 object를 labeling하고 풀어봅니다.
- 숫자 대입: 정답에 실제 숫자를 대입하여 성립하는지 확인합니다. 위 sampling table 예시를 들어보면,
- 일반적인 경우: k=1을 대입합니다. → $\binom{n}{1}$
- 극단적인 경우: k=0을 대입합니다. → $\binom{n-1}{0}$
- 계산하기 간단하지만 당연하지 않은 경우: n=2를 대입합니다. → $\binom{n+1}{k}$ = $\binom{k+1}{1}$ = $k+1$
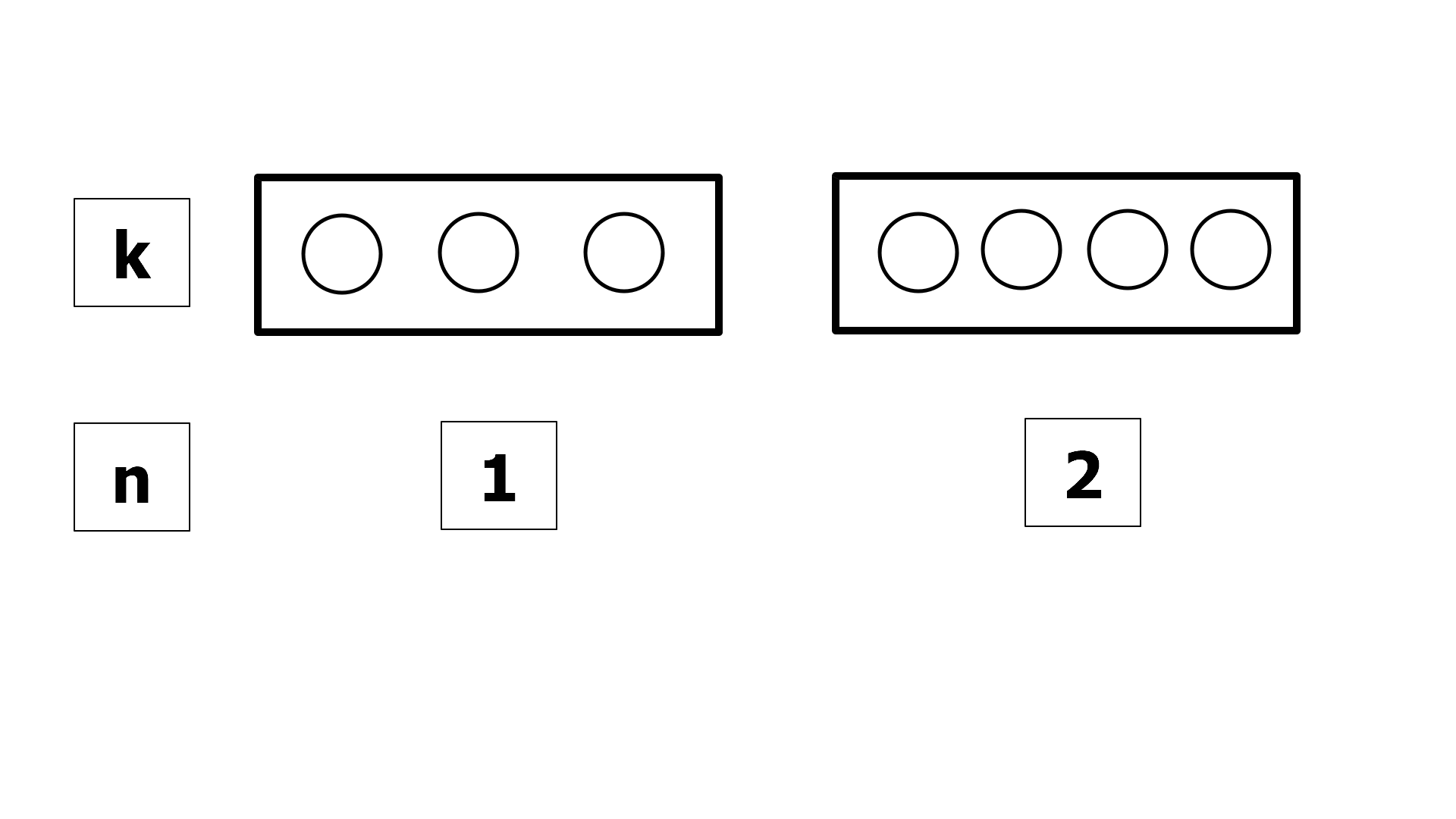
두 개의 상자가 있다고 가정합니다.(n=2) 상자를 선택할 때마다 상자 안에 dot으로 표시합니다. 총 7번을 선택합니다.(k=7) 이 때 첫 번째 상자에 dot을 표시할 수 있는 경우의 수는 0, 1, 2, …, k개로 총 k+1가지 입니다.
![Post-Image]() Example
Example - 일반화: n개의 상자에 k개의 구별 불가능한 object를 넣을 수 있는 경우의 수로 확장해 봅니다.
![Post-Image]() Example
Example
위 그림은 n개의 구슬을 k개의 상자에 넣는 경우의 수는 몇 가지인가?라는 물음에 대한 예시입니다. 구슬과 같이 실물이 있는 물체는 labeling이 가능하며 서로 구별이 가능합니다. 따라서 확률의 naive한 정의로 접근 가능합니다. 하지만 물리학과 같은 경우 object들이 항상 구별 가능한 것이 아니므로 이와 같은 접근이 어렵습니다. 따라서 아래 그림과 같은 경우로 변경하여 생각할 수 있습니다.
아래 그림은, n개의 원 사이에 k-1개의 구분선을 넣는 경우의 수는 몇 가지인가?라는 물음에 대한 예시입니다. n+k-1개의 위치에 구슬과 구분선을 배열하는 것과 같습니다.
원의 위치를 먼저 정하면 구분선의 위치가 결정됩니다. 구분선의 위치를 먼저 정하면 원의 위치가 결정됩니다. 따라서 다음 등식이 성립합니다.
$\binom{n+k-1}{n-1}$ = $\binom{n+k-1}{k}$
Story Proof
상황 해석을 통한 증명입니다.(Proof by interpretation) 다음과 같은 예시를 생각해 볼 수 있습니다.
$\binom{n}{k} = \binom{n}{n-k}$
앞서 증명한 내용과 같습니다. n개 중 k개를 선택하는 경우의 수는 n개 중 n-k개를 선택하는 경우의 수와 같습니다.$n\binom{n-1}{k-1} = k\binom{n}{k}$
n명 중 동아리에 들어갈 k명을 선발하고 그 중 한 명을 대표로 선정하는 경우를 생각해 봅니다.
좌변은 대표를 한 명 선정합니다. 이후 n-1명 중 동아리에 들어갈 k-1명을 선발합니다.
우변은 n명 중 동아리에 들어갈 k명을 선발합니다. 이후 k명 중 대표 한 명을 선정합니다.
두 수식이 같다는 것이 증명 되었습니다.$\binom{m+n}{k} = \sum_{j=0}^{k}\binom{m}{j}\binom{n}{k-j}$
이 수식은 Vandermonde 항등식으로도 부릅니다. 대수를 이용해 증명하는 것은 매우 복잡합니다. 이항정리로 증명하는 것도 매우 복잡합니다. Story proof를 통해 증명해 봅니다.
두 개의 그룹 m, n에서 각각 사람을 뽑아 총 k명을 뽑는 경우의 수를 생각합니다. 그룹 m에서 j명을 선택한 경우 그룹 n에서는 k-j명을 선택합니다. 중복으로 counting한 경우가 없으므로 multiplication rule에 따라 두 개 그룹에서 선별한 경우를 곱하고 j는 0~k명 까지 모든 경우의 수를 더해줍니다.
확률의 non-naive한 정의의 공의
Sample space S와 function P가 있습니다. Event A는 S의 부분집합이며 P는 A를 input으로 받아서 $P(A)\in[0,1]$을 output으로 내놓습니다.
이 정의를 만족시키기 위해서는 다음 두 가지 정리가 필요합니다.
$P(\emptyset)=0, p(S)=1$
$P(\cup_{n=1}^{\infin}A_{n}) = \sum_{n=1}^{\infin}P(A_{n})$ if $A_{1}, A_{2}$, … are disjoint (non-overlapping)
IMO
기억나는 재생만 헤아려도 4회 이상입니다. 재생할 때마다 새로운 내용이 들립니다. 간단한 내용처럼 보였지만 반복해서 들으니 놓쳤거나 이해하지 못했던 내용이 많았습니다. Story proof 방식이 아직 익숙하지 않지만 대수적으로 증명/해결하려는 시도보다 적극적으로 활용해야 겠다고 생각합니다.
 Example
Example 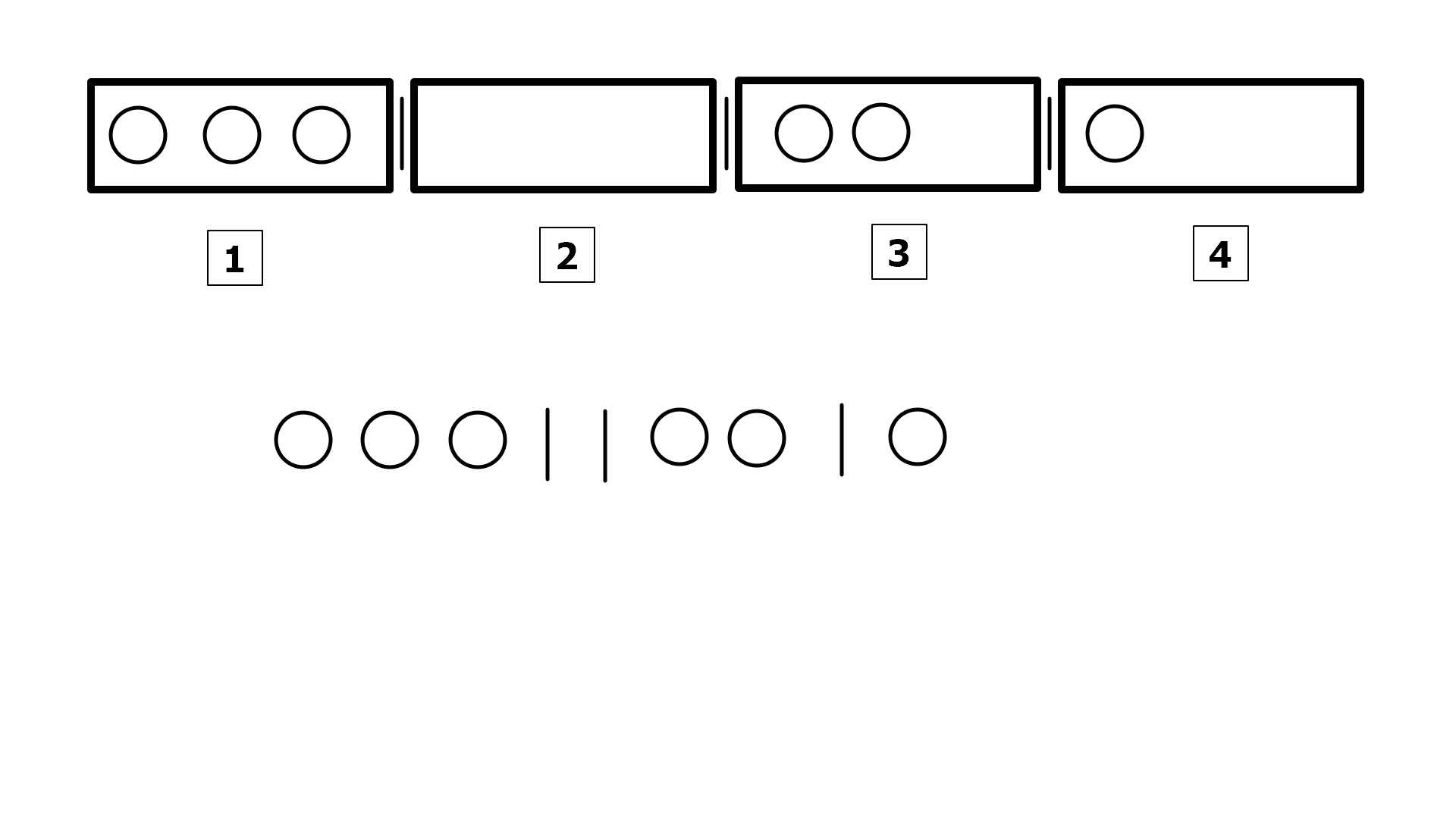 Example
Example