기약행 사다리꼴 행렬 (3.1)
가우스-조던 소거법을 사용해서 선형 연립방정식을 풀 수 있습니다. 가우스-조던 소거법은 임의의 행렬을 기약행 사다리꼴 행렬(RREF: Reduced Row Echelon Form)로 변환하여 연립방정식의 해를 쉽게 찾을 수 있습니다.
첨가행렬 (agumented matrix)
선형 연립방정식은 첨가행렬(augmented matrix)로 표현할 수 있습니다. 첫 번째 열은 첫 번째 변수의 계수, n 번째 열은 n 번째 변수의 계수, 그리고 마지막 열은 우변에 있는 상수를 의미합니다.
행 연산
다음과 같이 행렬의 행을 조작하여 행연산 수행 후 연립방정식 해를 구할 수 있습니다.
- 두 행의 위치를 교환합니다.
- 한 행에 상수를 곱합니다.
- 어느 한 행에 상수를 곱한 후 다른 행을 더합니다.
기약행 사다리꼴은 가장 간단한 첨가행렬 형태입니다. 각 행에는 피벗(pivot)이라고 하는 그 행에서 가장 먼저 나타나는 숫자 1(선행 1)이 있습니다. 각 열의 피벗은 동일한 열에서 아래/위 숫자를 제거하는데 사용됩니다. 이 과정을 거치면 결국 기약행 사다리꼴 형태가 됩니다.
정의
- 행렬의 j행에 대한 피벗은 j행의 가장 왼쪽에 있는 0이 아닌 성분입니다. 모든 피벗은 각 행에 적절한 숫자를 곱하여 선행 1로 변환할 수 있습니다.
- 가우스 소거법은 행렬을 행 사다리꼴 형태(REF)로 변환하는 과정입니다.
- 선행 1 아래의 모든 성분이 0이면 이 행렬은 행 사다리꼴 형식(REF)이라고 합니다.
- 가우스-조던 소거법은 행렬을 기약행 사다리꼴 형태(RREF)로 변환하는 과정입니다.
- 피봇 위/아래에 있는 모든 성분이 0이면 기약행 사다리꼴 형식(RREF)이라고 합니다.
- rank(A): 행렬 A의 랭크는 A의 RREF에 있는 피벗의 개수입니다.
가우스-조던 소거 알고리즘
가우스-조던 소거 알고리즘(Gauss-Jordan elimination algorithm)은 왼쪽에서 오른쪽으로 이동하는 순방향과, 오른쪽에서 왼쪽으로 이동하는 역방향의 두 단계로 진행됩니다.
순방향 단계(왼쪽에서 오른쪽)
- 맨 왼쪽 열에서 피벗(선행 1)을 얻습니다.
- 1단계의 피벗 아래에 있는 열의 모든 성분이 0이 되도록 그 아래의 모든 행에서 피벗이 있는 행을 뺍니다.
- 다음 열의 선행 1을 찾아 반복합니다.
역방향 단계(오른쪽에서 왼쪽)
- 맨 오른쪽 피벗을 찾아 이를 이용하여 해당 피벗 열에서 피벗 위의 모든 숫자를 제거합니다.
- 한 열 왼쪽으로 이동해서 반복합니다.
해의 개수
세 개의 변수를 갖는 세 개의 선형 연립방정식에서 서로 조건이 다른 경우를 알아봅시다.
해가 유일할 때
어떤 행렬의 RREF에 각 행마다 피벗이 있으면, 해를 바로 알 수 있습니다.
$\begin{vmatrix}
1 & 0 & 0 \bigm| c_{1}
0 & 1 & 0 \bigm| c_{2}
0 & 0 & 1 \bigm| c_{3}
\end{vmatrix}$유일한 해는 $x_{1} = c_{1}, x_{2} = c_{2}, x_{3} = c_{3}$ 입니다.
해가 무수히 많을 때
방정식 중 하나가 중복되면 RREF로 변환된 행렬에 0으로만 이루어진 행이 나타납니다. 이것은 원래 방정식 중 하나가 나머지 두 방정식에 대해 선형결합일 때 발생합니다. 이 경우에는 세 개의 변수로 두 개의 방정식을 풀어야 하므로, 알려지지 않은 변수 중 하나를 고정할 수 없습니다. 이때 해가 자유 변수를 포함한다고 합니다.
$\begin{vmatrix}
1 & 0 & a_{1} \bigm| c_{1}
0 & 1 & a_{2} \bigm| c_{2}
0 & 0 & 0 \bigm| 0
\end{vmatrix}$$x_{3} = t$가 자유 변수이며 $-\infin$와 $\infin$사이의 어떤 값을 취할 수 있습니다. $x_{1} = c_{1} - a_{1}t, x_{2} = c_{2} - a_{2}t$로 표현할 수 있습니다.
2차원에서 해가 무수히 많을 때
0이 아닌 3개의 방정식이 모두 일치할 때 발생합니다. 그 결과 하나의 선행 1과 두 개의 자유 변수가 생깁니다.
해가 존재하지 않는 경우
3개의 방정식을 모두 동시에 만족하는 수 $x_{1}, x_{2}, x_{3}$가 없다면, 연립방정식의 해는 존재하지 않습니다. RREF 형식에서 계수가 모두 0인 행을 포함하고, 우변에 0이 아닌 상수인 경우에는 해가 없습니다.
기하학적 해석
2차원 상의 직선
방정식 $ax + by = c$는 $\mathbb{R}^2$ 상의 직선입니다. 두 개의 연립방정식이 있을 때 해를 찾기 위해서는 두 직선이 교차하는 점 (x, y)를 찾아야 합니다. 해집합은 세 가지 경우가 있습니다.
- 하나의 해: 두 직선이 한 점에서 교차하는 경우
- 무수히 많은 해: 두 직선이 겹치는 경우
- 해가 존재하지 않음: 두 직선이 평행하고 교차하지 않는 경우
3차원 상의 평면
방정식 $ax + by + cz= d$는 $\mathbb{R}^3$ 상의 평면입니다. 세 개의 연립방정식이 있을 때 해를 찾기 위해서는 세 개의 방정식을 동시에 만족하는 점 (x, y, z)를 찾아야 합니다. 해집합은 네 가지 경우가 있습니다.
- 단 하나의 해: 평행하지 않은 세 개의 평면이 한 점에서 만나는 경우
- 1차원의 무수히 많은 해: 세 개의 평면 중 두 평면이 일치하는 경우, 평행하지 않은 두 평면은 직선으로 표차하며 하나의 직선에서 만남
- 2차원의 무수히 많은 해: 세 개의 평면이 모두 일치하고 0이 아닌 식일 경우, 해집합은 평면임
- 해가 존재하지 않는 경우: 세 개의 평면이 교차점이 없는 경우
행렬방정식 (3.2)
선형 연립방정식 문제를 행렬방정식으로 표현한 다음 역행렬을 사용하여 해를 구할 수 있습니다.
$x_{1} + 2x_{2} = 5$
$3x_{1} + 9x_{2} = 21$
이 연립방정식을 행렬-벡터 곱으로 다시 쓸 수 있습니다.
$\begin{bmatrix} 1 & 2
3 & 9 \end{bmatrix}$ $\begin{bmatrix} x_{1}
x_{2} \end{bmatrix}$ = $\begin{bmatrix} 5
21 \end{bmatrix}$
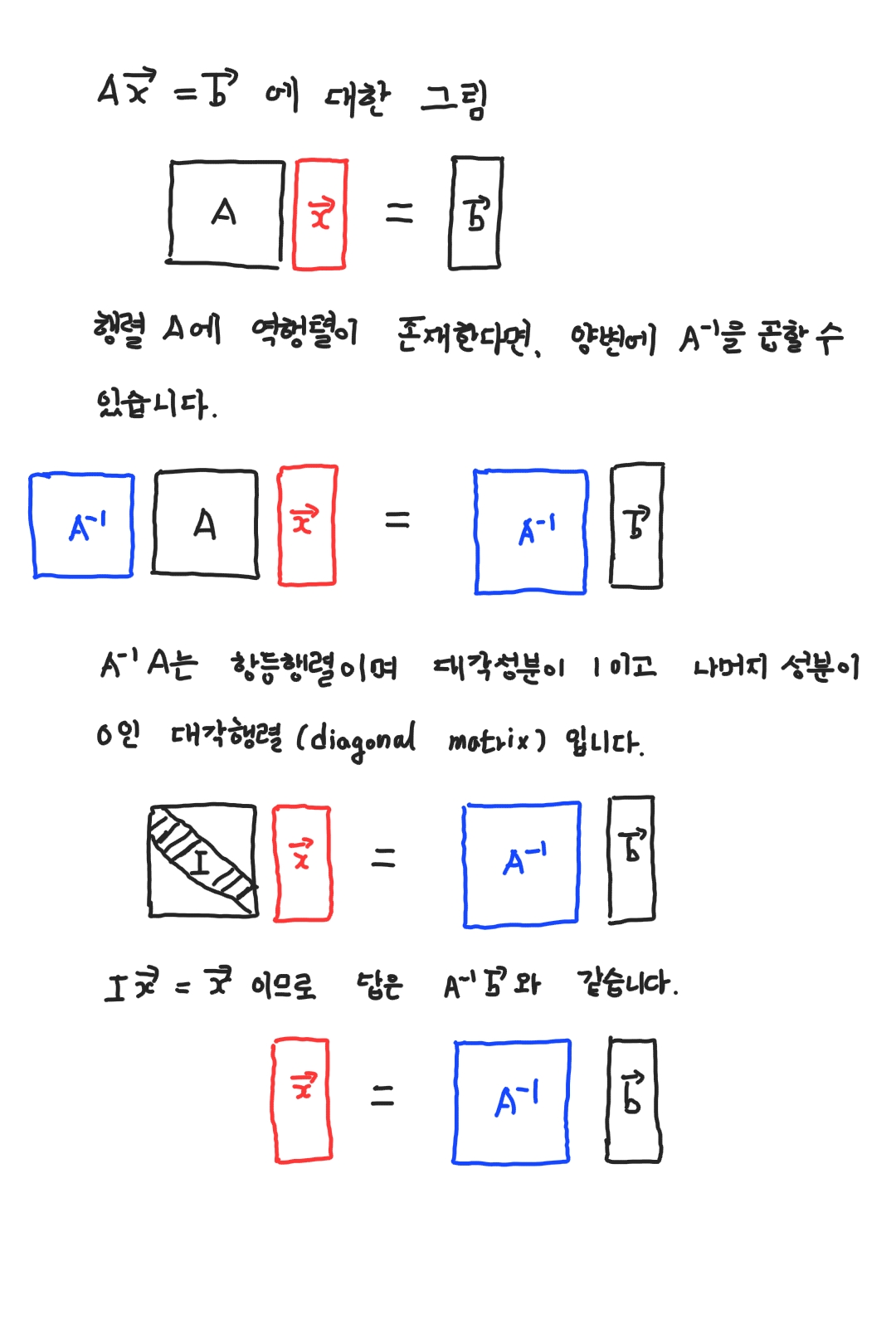
더 간단하게 $A\vec{x} = \vec{b}$로 나타낼 수도 있습니다. 여기서 A는 2x2 행렬, $\vec{x}$는 미지수 벡터(2x1 행렬), $\vec{b}$는 상수 벡터(2x1 행렬)입니다. 이 행렬방정식의 양변에 역행렬 $A^{-1}$를 곱하여 $\vec{x}$를 풀 수 있습니다.
$A^{-1}A\vec{x} = \mathbb{I}\vec{x} = \vec{x} = A^{-1}\vec{b}$
따라서, 계수 행렬의 역행렬을 구한 후에 곱을 계산하여 선형 연립방정식을 풉니다.
$A^{-1}$를 찾는 데 들이는 노력은 첨가행렬 $[A \mid \vec{b} ]$를 RREF로 변환하는 데 들이는 노력과 비슷합니다. 연립방정식을 행렬 형태로 변환해서 해를 구하면 수십 개의 계수를 각각 계산하지 않아도 된다는 점에서 유용합니다. A가 2x2 행렬이든 1000x1000 행렬이든 행렬의 크기와 상관없이 같은 식 $\vec{x} = A^{-1}\vec{b}$가 적용됩니다.
행렬과 벡터의 곱
방정식 $A\vec{x} = \vec{b}$를 푼다고 가정해 봅시다. 이는 nxn행렬 A를 벡터 $\vec{x}$에 곱하여 벡터 $\vec{b}$를 생성한다는 의미입니다. 벡터는 ‘높고 좁은’ nx1 행렬로 생각할 수 있습니다.
![Post-Image]()
행렬과 벡터의 곱 $A\vec{x} = \vec{b}$에서 때때로 행렬 A의 역행렬이 존재하지 않는 경우가 있습니다. 연립방정식이 부족하게 설정된 경우(A가 높이보다 더 넓은 경우), 가능한 해 $\vec{x}$의 부분공간(subspace)이 존재합니다. 이전 절에서 살펴본 해가 무수히 많은 경우에 해당합니다.
행렬과 벡터의 곱 행렬곱셈 (3.3)
행렬의 곱셈은 행렬 A의 각 행과 행렬 B의 각 열 사이에 내적을 취하여 계산합니다.
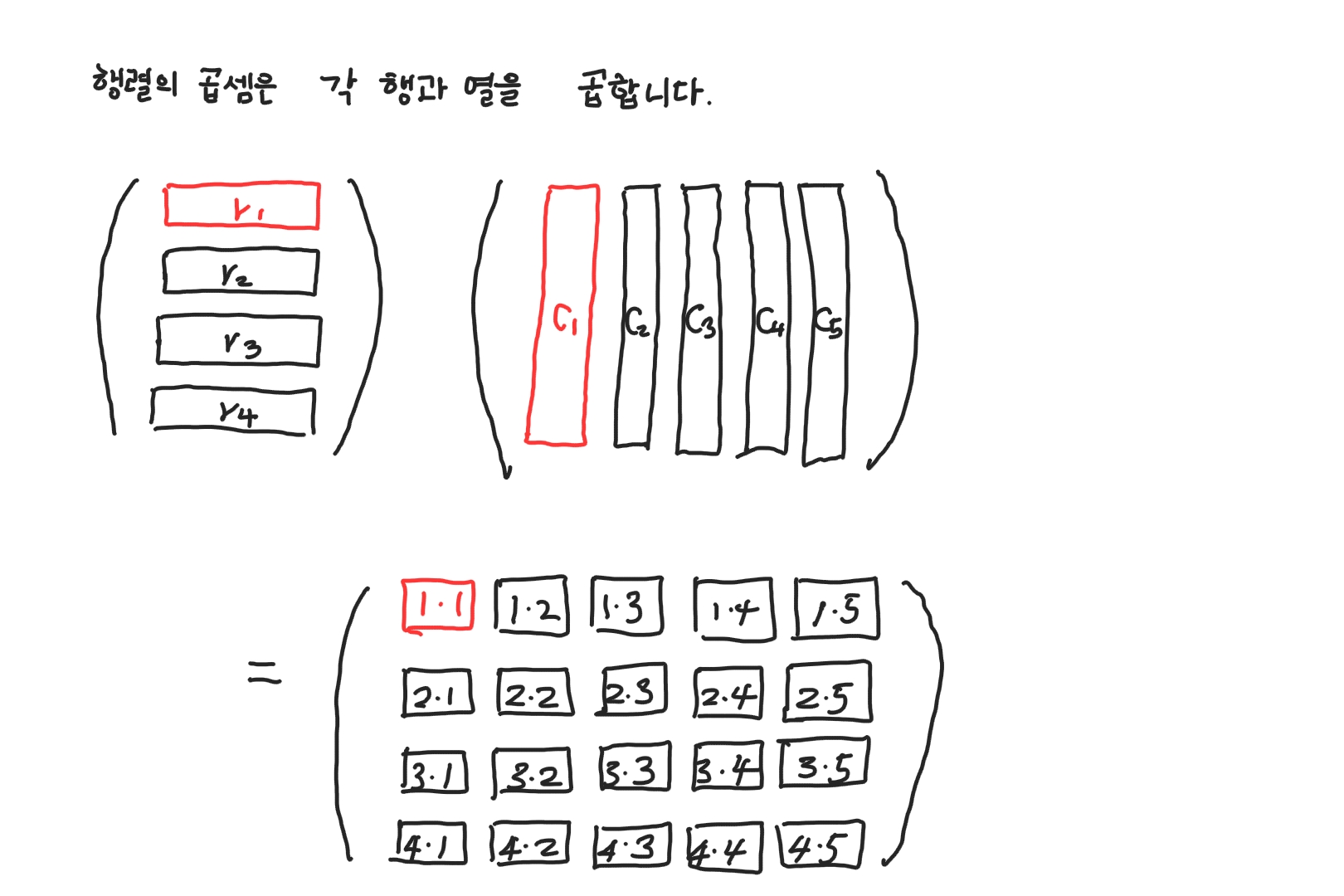행렬의 곱셈
행렬의 곱셈 법칙
- 행렬의 곱셈은 결합법칙이 성립합니다.
- 접촉하는 열과 행은 각각 크기가 동일해야 합니다.
- 행렬의 곱셈은 교환법칙이 성립하지 않습니다.
선형변환의 구성
행렬의 곱셈이 이러한 방식으로 정의되는 이유는 무엇일까요?
이 질문에 대한 제대로 된 대답은 선형변환에서 자세히 다루게 될 것입니다. 열벡터 $\vec{x} \in \mathbb{R}^n$를 행렬 $A \in \mathbb{R}^{m \times n}$에 곱하는 것은 선형변환 $T_{A}$를 적용하는 것과 비슷합니다.
$T_{A} : \mathbb{R}^{n} \to \mathbb{R}^{m}$
선형변환 $T_{A}$를 입력 $\vec{x}$에 적용하는 것은 행렬과 벡터의 곱 $A\vec{x}$를 계산하는 것과 동일합니다. $\mathbb{R}^{n}$에서 $\mathbb{R}^{m}$으로의 모든 선형변환은 어떤 행렬 $A \in \mathbb{R}^{m \times n}$와 같은 행렬 곱으로 설명할 수 있습니다.
행렬식 (3.4)
어떤 행렬 A의 행렬식은 det(A) 또는 $\mid A \mid$라고 표시하며, 행렬의 성분들을 곱해 결과값이 숫자가 되는 특별한 방법입니다. 다음과 같은 의미를 가집니다.
도형의 부피
행렬식을 기하학적 계산으로서 직관적으로 해석할 수 있습니다. 어떤 도형의 면이 행렬의 행이라면, 행렬식은 그 도형의 부피입니다.
2x2 행렬의 경우, 행렬식은 평행사변형의 넓이입니다.
3x3 행렬의 셩우, 행렬식은 평행육면체의 부피입니다.
차원 d>3에 대해서, 행렬식은 d차원의 초부피(hyper-volume)를 측정합니다.
선형변환 비례인자(scale factor)
행렬 $A_{T}$와 행렬-벡터 곱 $T(\vec{x}) \equiv A_{T}\vec{x}$로 정의된 선형변환 $T : \mathbb{R}^{2} \to \mathbb{R}^{2}$에서, 행렬식은 선형변환 T와 연관된 비례인자(scale factor)입니다. 비례인자는 입력공간에서 단위 정사각형(1x1 차원의 사각형)의 넓이가 T로 인해 어떻게 변환되는지 설명합니다. T를 통과한 후, 단위 정사각형은 det($T_{A}$)의 넓이를 갖는 평생사변형으로 변환됩니다.
선형독립성 검사
주어진 벡터 집합에 대해 선형독립성을 검사할 때 사용합니다. 벡터를 행렬의 행으로 하여 행렬을 구성하고 행렬식을 계산합니다. 행렬식이 0이 아닌 경우, 벡터는 선형독립입니다.
역행렬 존재 여부
역행렬이 존재하는지 여부를 알려줍니다. 만약 행렬식이 0이 아니면 행렬은 역행렬이 존재하며, 0이면 역행렬이 존재하지 않습니다.
이 외에도 벡터 외적과 관련 있으며, 고윳값 방정식의 정의에도 사용됩니다.
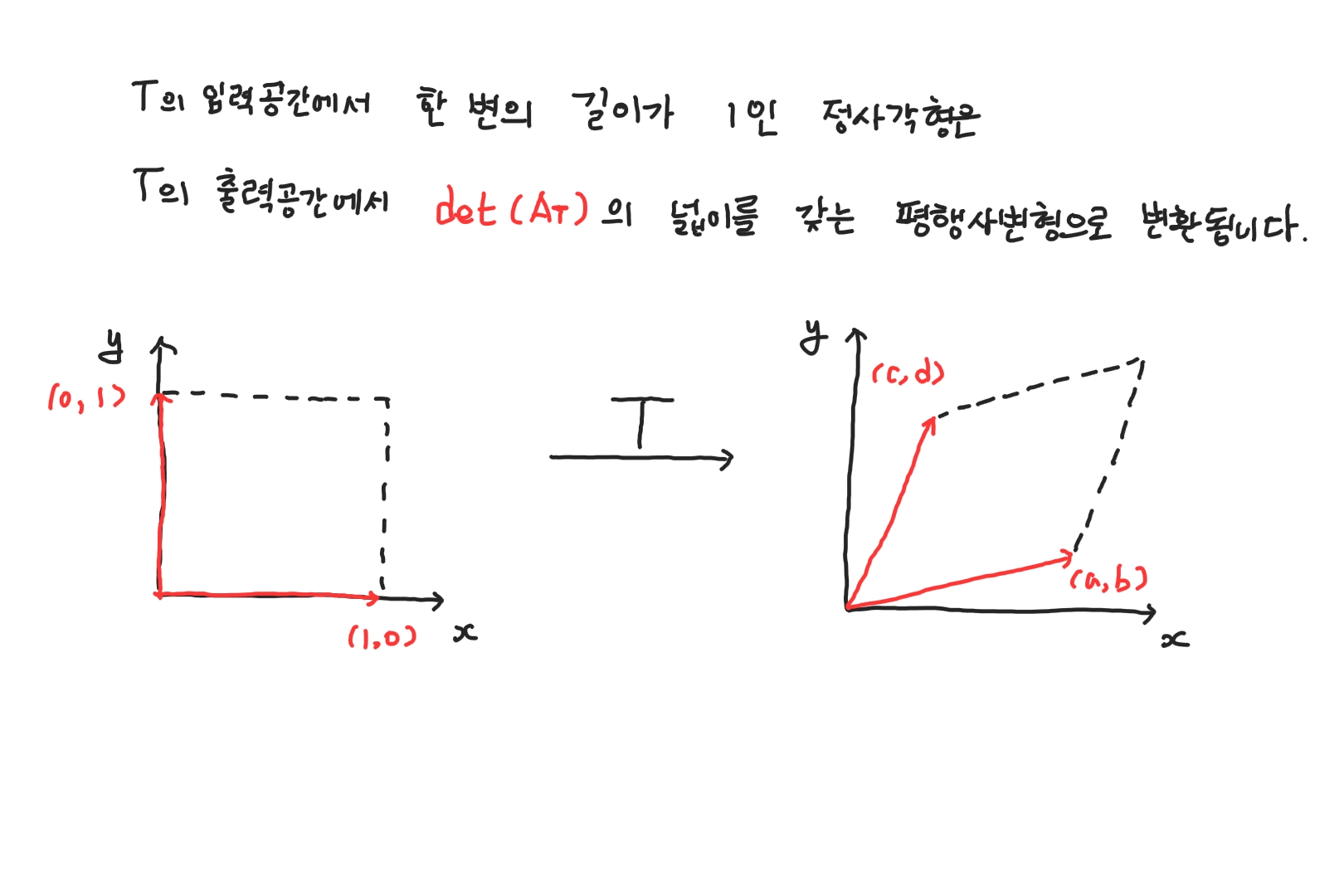햏렬식이 선형변환 비례인자로 작용
- 행렬식 공식
2x2 행렬의 행렬식은 다음과 같습니다.
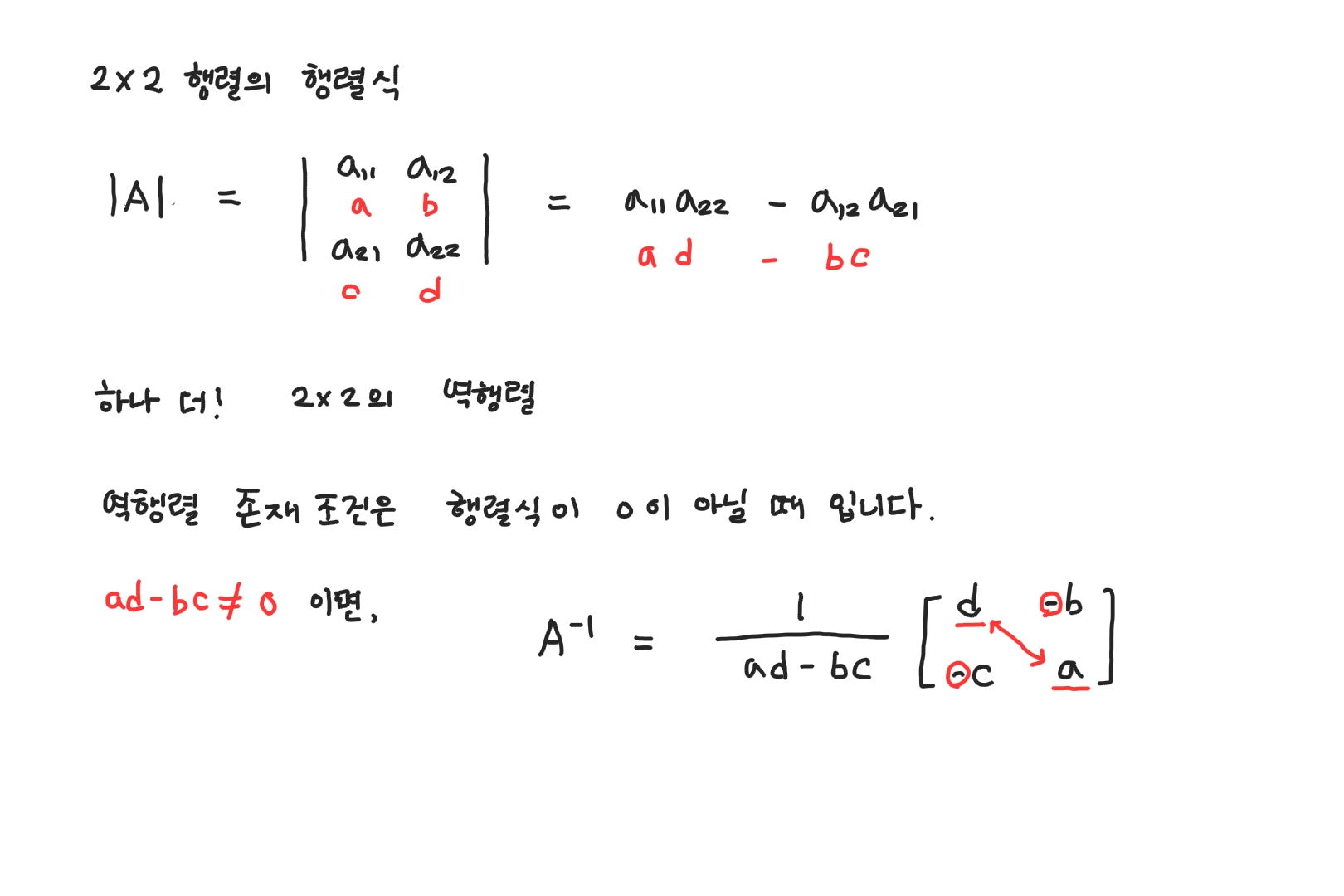2x2 행렬의 행렬식
3x3 행렬의 행렬식은 다음과 같습니다.
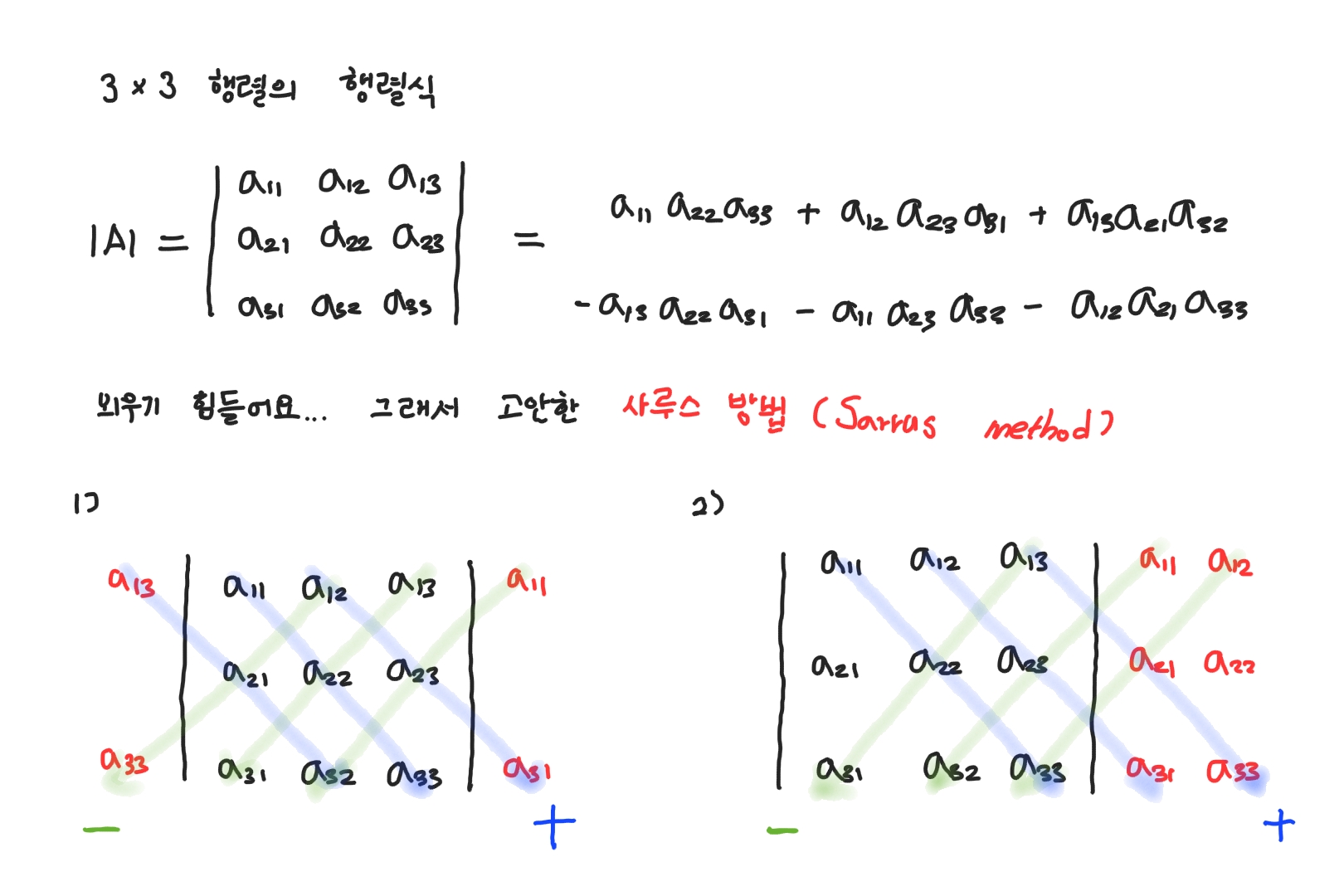3x3 행렬의 행렬식, Sarrus Method
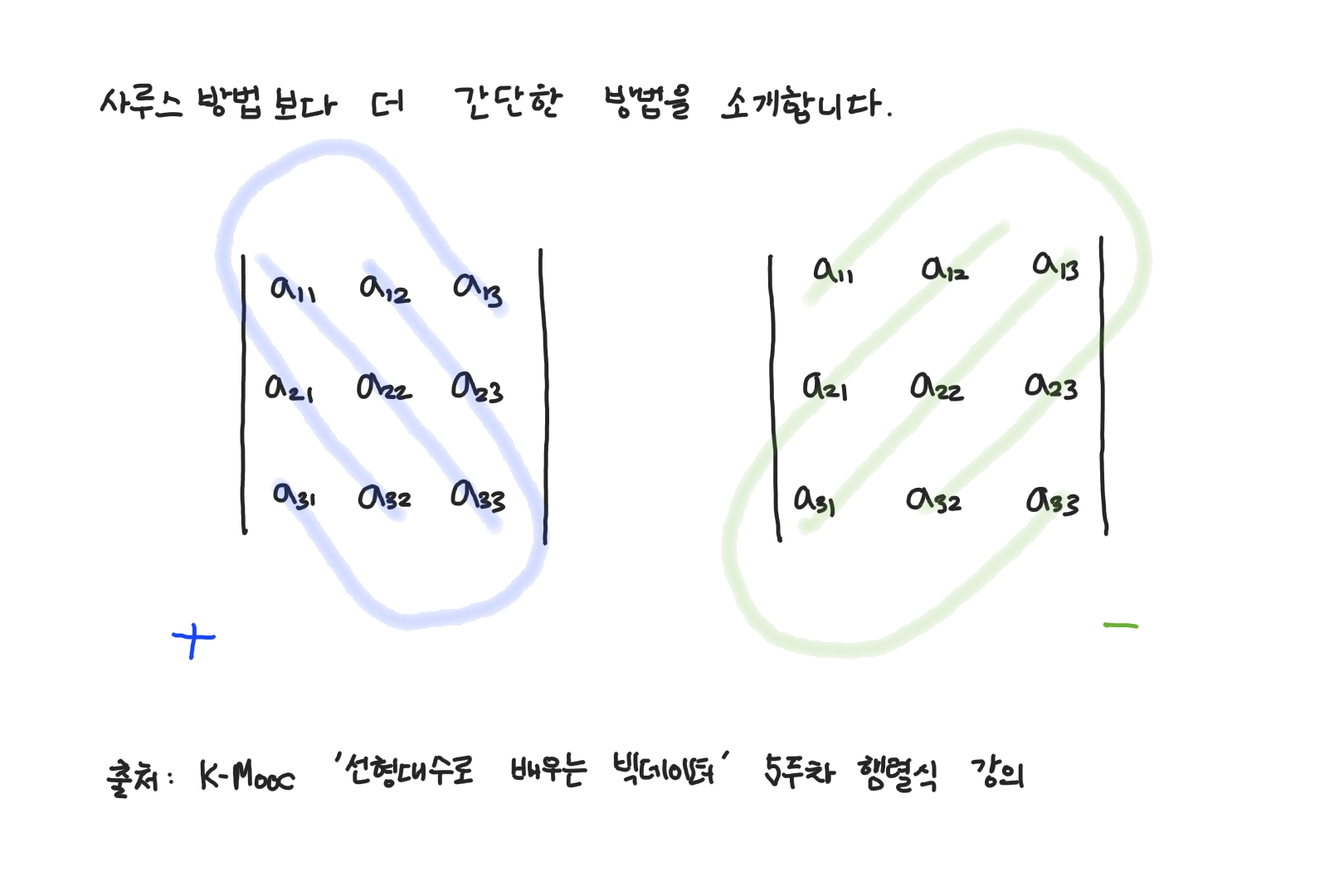3x3 행렬의 행렬식 쉽게 구하기
$n \times n$ 행렬의 행렬식은 더이상 쉬운 공식으로 간략히 구하기 어렵습니다. 대신 체계적으로 구할 수 있는 과정을 알아봅니다.
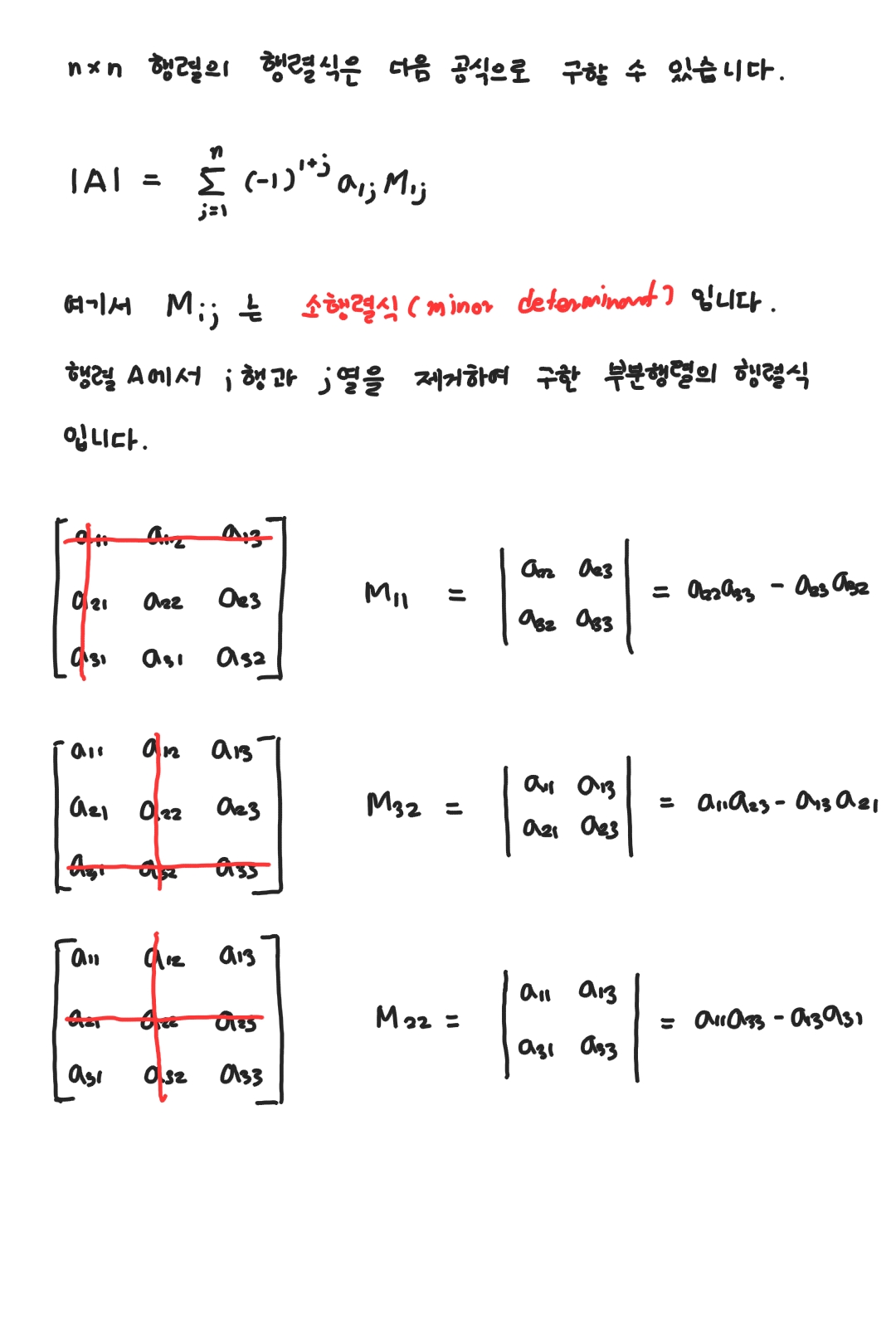nxn 행렬의 행렬식
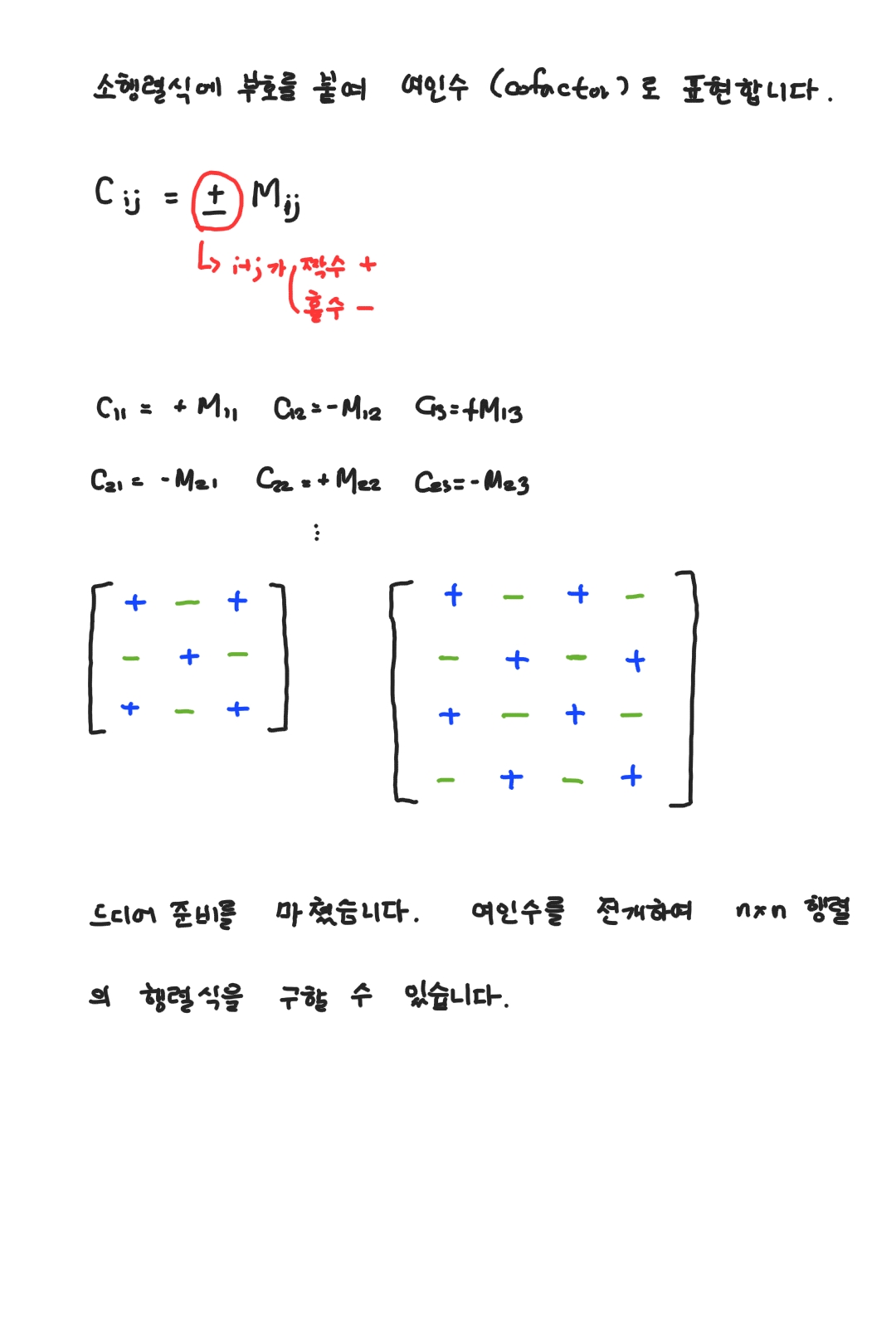nxn 행렬의 행렬식
nxn 행렬의 행렬식