Intro
사건의 독립(independence)과 조건부 확률(conditional probability)의 개념을 이해하고 적용할 수 있습니다.
Independence
독립의 정의는 다음과 같습니다.
Events A, B are independnet if $P(A \cap B) = P(A)P(B)$
Note: completely different from disjointness(서로소)
사건 A, B가 독립이라면 사건 A의 발생은 B의 발생 여부에 어떤 영향도 끼치지 않습니다.
혼동하기 쉬운 개념으로 서로소(disjoint)가 있습니다. 사건 A, B가 서로소라면 A가 발생했을 때 B는 발생할 수 없는 경우입니다. 독립과 완전히 다른 개념입니다.
Newton-Pepys Problem (1963)
Samuel Pepys는 유명한 작가입니다. 어느 날 도박에 관한 한 가지 문제에 대한 답을 얻기 위해 Newton에게 편지를 썼습니다.
여섯 개의 면이 나올 확률이 동일한 정육면체 주사위가 있습니다. 다음 세 가지 경우 중 가장 확률이 높은 것은 무엇일까요?
1
2
3
4
5
A. at least one 6 with 6 dice
B. at least two 6's with 12 dice
C. at least three 6's with 18 dice
‘at least’라는 표현이 나오면 합집합을 떠올립니다. 또한 합집합의 여집합은 교집합니다. 모든 사건이 독립이므로 교집합은 각 사건 확률의 곱셈으로 계산할 수 있습니다.
$P(A) = 1 - (\frac{5}{6})^6 \approx 0.665$
- $P(B)$ = 1 - (6이 한 번도 안 나올 확률 + 6이 딱 한 번 나올 확률)
$= 1 - {(\frac{5}{6})^{12} + \frac{1}{6} * (\frac{5}{6})^{11} * 12} \approx 0.619$ - $P(C) = 1 - \Sigma_{k=0}^{2}(\frac{18}{k})(\frac{1}{6})^k(\frac{5}{6})^{18-k} \approx 0.597$
따라서 A가 발생할 확률이 가장 높습니다.
Conditional Probability
Conditioning is the soul of statistics.
How should you update probability/beliefs/uncertainty based on new evidence? Contional probability는 새로운 정보를 얻었을 때, 기존에 가지고 있던 probability/beliefs/uncertainty를 어떻게 업데이트 하는가? 에 대한 답을 찾는 과정입니다.
정의는 아래와 같습니다. $P(A \mid B) = \frac{P(A \cap B)}{P(B)}, if P(B)>0$
정의를 이해하기 위해 두 가지 다른 직관적 접근을 알아보겠습니다.
직관적 접근 1) 조약돌 세계관
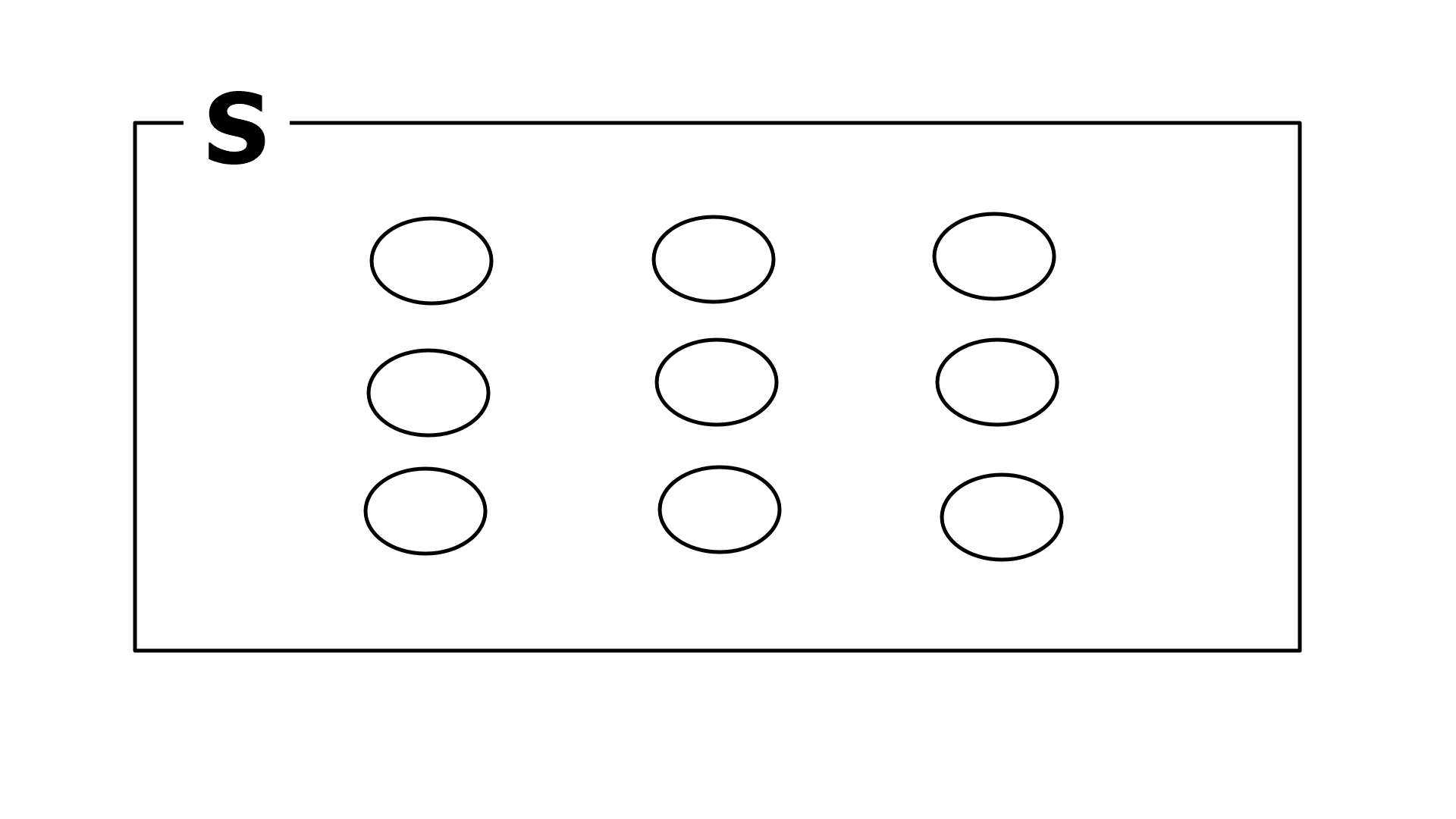조약돌 세계관
S 안에 q개의 조약돌이 있습니다. q개 조약돌들이 질량의 합은 1이라고 가정합니다.
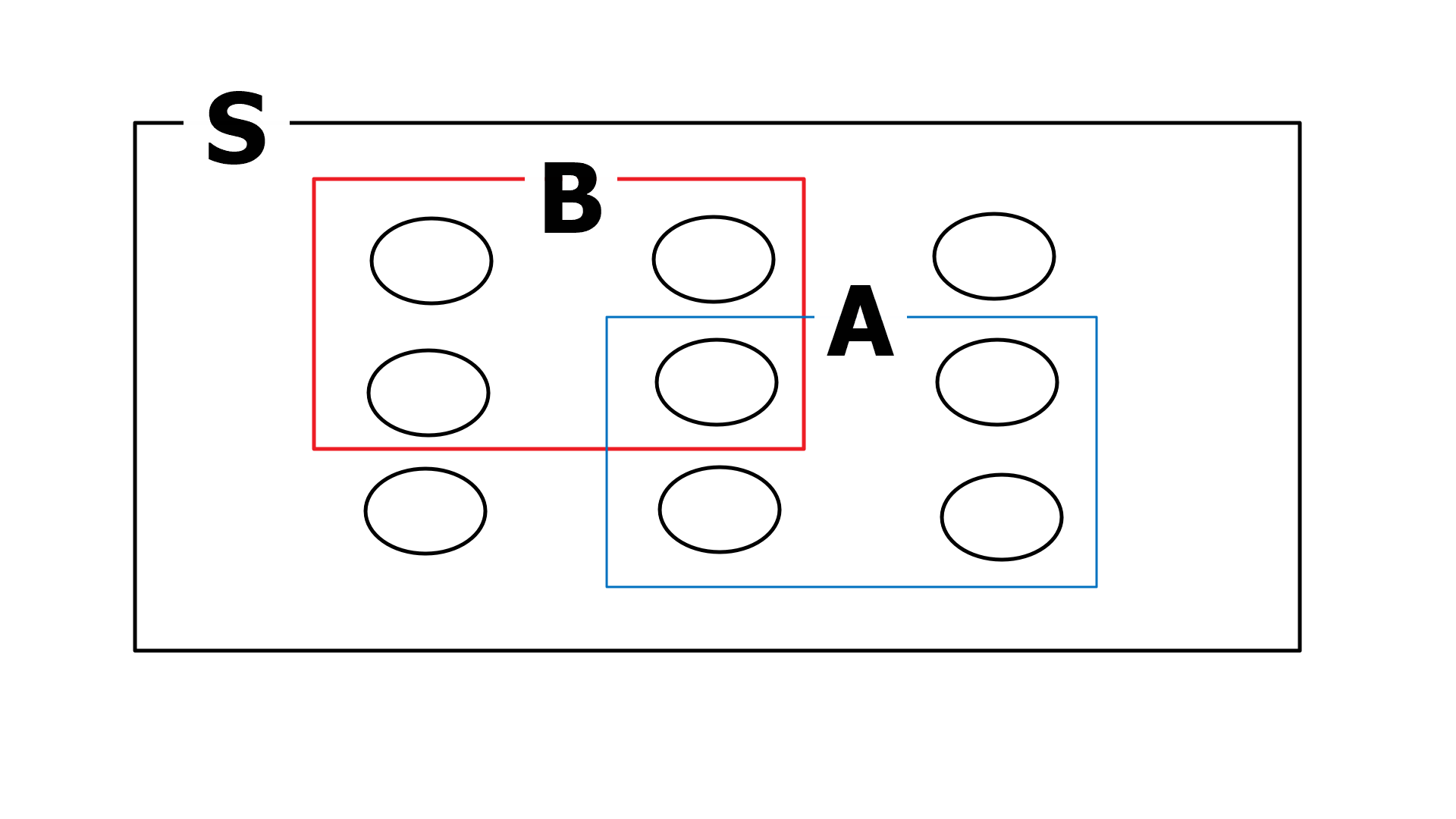조약돌 세계관
$P(A \cup B) = P(A \mid B)P(B)$ 경우를 생각해 봅니다. $P(A \mid B)$의 의미는, $B^{c}$에 있는 모든 조약돌을 무시하고 B가 새로운 조약돌 세계라고 가정할 때 B 안에서 A도 발생할 확률입니다. 그런데 B에 있는 조약돌들의 질량의 합이 1이 안되기 때문에 재규격화(renormalize, 어떤 상수를 곱하여 전체 질량의 합이 다시 1이 되도록 하는 것)합니다. 따라서 $P(A \cap B)$를 P(B)로 나누어 줍니다.
$P(A \mid B) = \frac{P(A \cap B)}{P(B)}, if P(B)>0$
직관적 접근 2) 빈도학파(Frequentist) 세계관
같은 실험을 계속 반복하여 수 많은 시행 끝에 얻어낸 사건이 일어나는 비율을 확률로 보는 세계관 입니다. 따라서 왜 확률을 $\frac{P(A \cap B)}{P(B)}$ 식에 따라 계산하는지 알 수 있습니다. B 사건 하에서 A 사건이 발생할 확률은, A와 B가 함께 일어날 확률을 B가 일어날 확률로 나눠주는 것입니다.
직관적 접근의 결과를 아래와 같이 정리할 수 있습니다.
정리 1) $P(A \cap B) = P(B)P(A \mid B) = P(A)P(B \mid A)$
정리 2) $P(A_{1}, A_{2}, …, A_{n}) = P(A_{1})P(A_{2} \mid A_{1})P(A_{3} \mid A_{1},A_{2}) … P(A_{n} \mid A_{1}, …, A_{n-1})$
정리 3) $P(A \mid B) = \frac{P(B \mid A)P(A)}{P(B)}$, Bayes’ Theorem (베이즈 정리)
IMO
확률론에서 중요한 이론 중 하나로 자주 등장하는 Bayes’ theorem(베이즈 정리)의 정의와 의미를 배웠습니다.