Intro
전체 확률의 법칙을 이해하고 문제풀이에 적용할 수 있으며, 조건부 독립의 개념을 이해합니다.
How to Solve the Problem
어떤 문제를 풀 때 다음 두 가지 방법을 적용해 볼 수 있습니다.
- 간단한 케이스와 극단적인 케이스에 적용해보기
- 문제를 작은 문제들로 쪼개서 생각해보기
Law of Total Probability (전체 확률의 법칙)
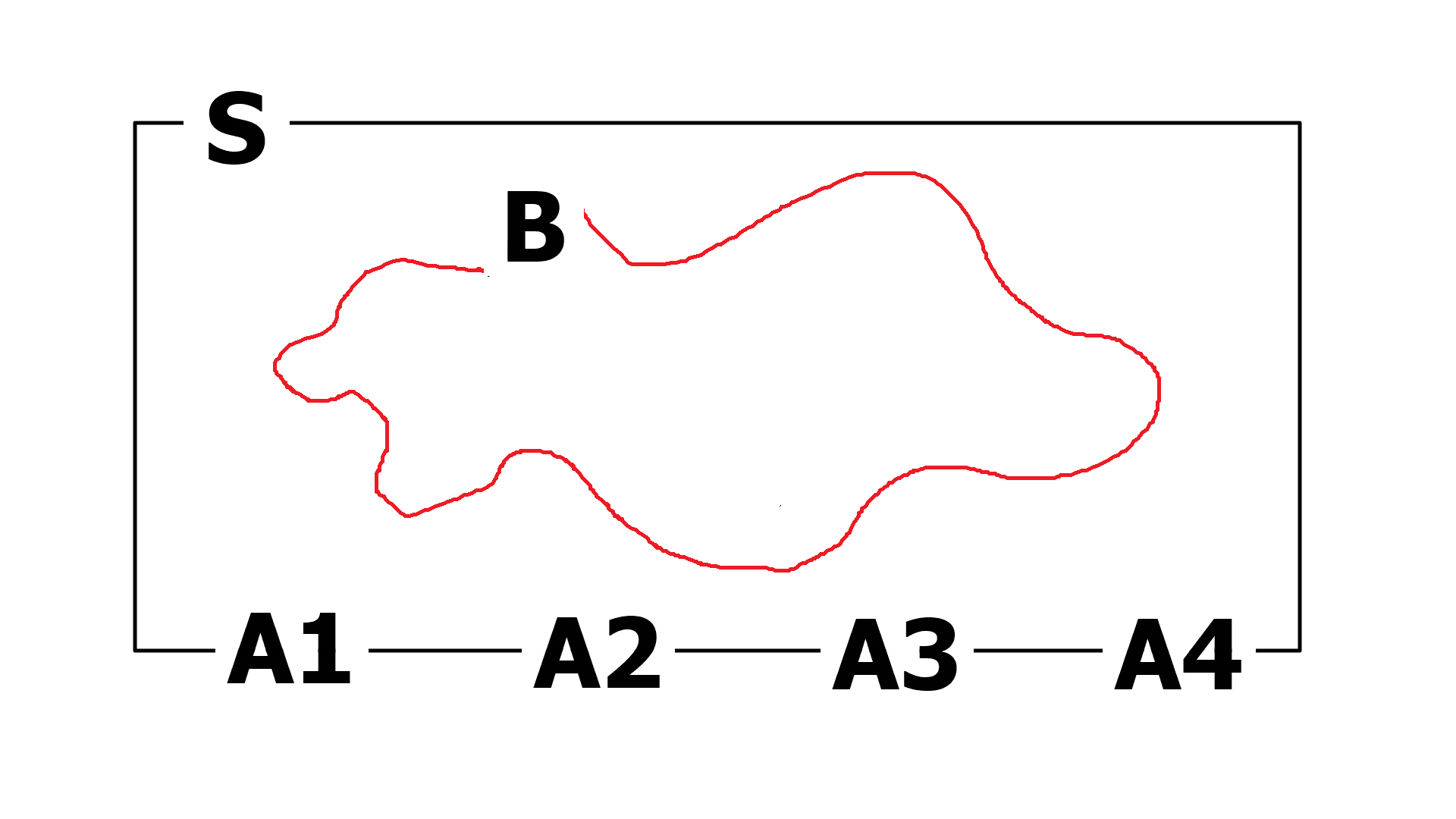law of Total Probability
$P(B \mid S)$를 구할 때, S를 서로소 관계에 있는 $A_{1}, A_{2}, A_{3}, A_{4}$로 쪼개서 계산하면 쉽게 구할 수 있습니다. 이것을 low of total probability (전체 확률의 법칙) 이라고 합니다.
$P(B) = P(B \cap A_{1}) + P(B \cap A_{2}) +, …, + P(B \cap A_{n})$
$ = P(B \mid A_{1})P(A_{1}) + P(B \mid A_{2})P(A_{2}), …, + P(B \mid A_{n})P(A_{n})$
Conditional Probability가 중요한 이유
It’s own right!
조건부 확률은 어떤 단서가 있을 때 이 단서를 기반으로 확률을 업데이트 하는 것입니다. 이 자체가 굉장히 중요한 개념입니다.Unconditional probability를 구하기 위해 이를 작은 조각들로 쪼갤 때 conditional probability가 필요합니다.
예를 들어 Unconditional probability인 P(B)를 구하기 위해서 $P(B \mid A_{1})P(A_{1}) + P(B \mid A_{2})P(A_{2}), …, + P(B \mid A_{n})P(A_{n})$와 같이 conditional probability인 $P(B \mid A_{n})$이 필요합니다.
Conditional Probability 예제 문제
- 카드 뽑기: 52장의 카드 중 2장의 카드를 뽑는 경우, 다음 두 가지 case를 생각해 봅니다.
$P(both aces \mid have an ace)$
$= \frac{P(both aces)}{P(have ace)}$
$= \frac{\binom{4}{2}/\binom{52}{2}}{1 - \binom{48}{2}/\binom{52}{2}}$
$= \frac{1}{33}$$P(both aces \mid have an ace of spade)$
$= \frac{3}{51}$
$= \frac{1}{17}$
한 장의 카드는 spade ace로 정해져 있으므로, 나머지 한 장의 카드를 남은 ace 세 장 중 하나를 뽑을 확률입니다.
- 환자가 병에 걸렸을 확률: 인구의 1%가 걸리는 병이 있습니다. 이 병을 검사하는 방법 정확도가 95%라고 가정합니다. 검사가 양성으로 나왔을 때 환자가 병에 걸렸을 case를 생각해 봅니다.
D: 환자가 병을 가지는 경우
T: 환자의 검사 결과가 양성인 경우
$P(T \mid D) = 0.95$
$P(T^{c} \mid D^{c})$
하지만 환자가 알고자 원하는 것은 무엇일까요? 바로 $P(D \mid T)$입니다.
$P(D \mid T) = \frac{P(T \mid D)P(D)}{P(T)}$
$\frac{P(T \mid D)P(D)}{P(T \mid D)P(D) + P(T \mid D^{c})P(D^{c})}$
$\approx 0.16$
Conditional Probability에서 자주 하는 실수들
Prosecutor’s fallacy: $P(A \mid B)$와 $P(B \mid A)$를 혼동하는 case입니다. 법정 사례를 한 가지 살펴봅니다.
Sally Clark case: 영국인 Sally Clark의 두 아이가 영아돌연사증후군(SIDS)로 돌연 사망합니다. 검찰측 전문가는 아이가 설명하기 힘든 이유로 사망할 확률은 $\frac{1}{8500}$이라 설명했고 두 명의 아이가 사망했으니 $\frac{1}{8500}\frac{1}{8500} \approx \frac{1}{73*10^6}$의 확률로 그녀가 결백하다고 주장했습니다.
하지만 우리가 알아야 할 값은 $P(innocence \mid evidence)$이며 위 주장에서는 $P(innocence)$ 항목을 고려치 않고 있습니다. 또한 두 아이의 죽음이 유전적 결함 등으로 연결될 수 있으나 검찰측 전문가는 독립사건으로 가정하고 있습니다. 결국 Sally Clark는 몇 년 후 무죄로 판정되어 출소했으나 얼마 지나지 않아 사망했습니다.사전확률(prior)과 사후확률(posterior) 혼동: 사전확률(prior)은 $P(A)$, 사후확률(posterior)은 $P(A \mid B)$입니다.
Conditional independent와 Independent 혼동: Conditional independent의 정의는 다음과 같습니다. $P(A \cap B \mid C) = P(A \mid C)P(B \mid C)$
그렇다면 conditional independent하면 independent 할까요? 정답은 ‘아니오’ 입니다.
체스 게임을 예로 들어봅시다. 실력을 알 수 없는 만나본 적 없는 상대와 체스 게임을 합니다. 상대방이 얼마나 체스를 잘 하는지 아무런 정보가 없습니다. 이렇게 상대방의 실력을 모르는 상태에서 체스 게임을 한다고 가정할 때 체스 게임들은 conditional independent 합니다. 하지만 이것이 independent를 의미하지 않습니다. 체스 게임을 반복할 수록 상대방의 실력을 가늠할 수 있는 척도가 마련되지 때문입니다.
반대로 independent하면 conditional independent 할까요? 정답은 ‘아니오’ 입니다.
화재경보기 예제를 생각해 봅시다. 화재경보기가 울리는 사건을 A, 화재가 난 사건을 F, 팝콘을 튀기는 사건을 C라고 합니다. A는 F 혹은 C에 의해 일어나며 F, C는 independent 하다고 가정합니다. 여기서 $P(F \mid A, C^{c}) = 1$이라고 할 수 있습니다. 화재경보기가 작동한 조건에서 팝콘을 튀기지 않았다면 화재가 났음을 알 수 있습니다. 따라서 A 조건하에서 F, C는 dependent하다고 볼 수 있습니다.
IMO
Conditional Probability를 확실하게 체득하지 못했으나 반복해서 강의를 듣고 다른 도서 내용도 참고해봐야 겠습니다.