Intro
Monty Hall 문제를 이해하고 확장해 볼 수 있으며, 심슨의 역설을 이해합니다.
Monty Hall Problem
Monty Hall 문제는 Monty가 사회를 맡은 유명한 퀴즈쇼 프로그램입니다. 1, 2, 3번 3개의 문이 있고 그 뒤에 자동차 한 대, 염소 두 마리가 있습니다. 참가자는 우선 문 1개를 선택합니다. Monty는 나머지 2개 문 중 염소가 들어있는 한 개의 문을 엽니다. 그리고 참가자에게 선택을 변경할 수 있는 기회를 줍니다. 이 때 참가자는 선택을 변경하는 것이 유리할까요, 아니면 처음 선택을 유지하는 것이 유리할까요?
Monty Hall 풀이1: 수형도
수형도를 그려서 확률을 계산해 볼 수 있습니다.
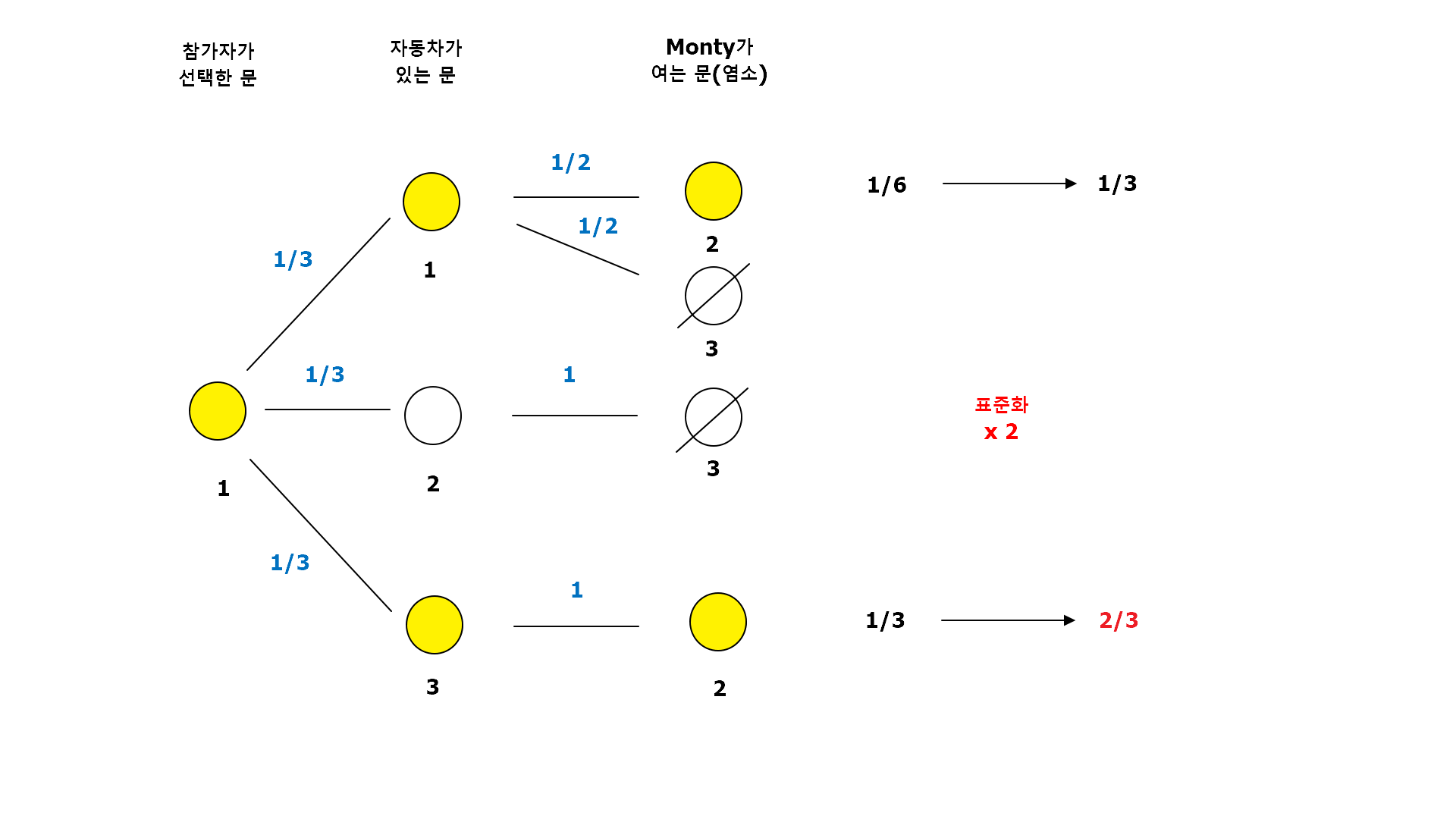
참가자가 1번 문을 선택했다고 가정합시다. Monty는 염소가 들어있는 2번 문을 엽니다. 이 때 참가자가 선택을 변경하지 않으면 자동차가 있는 문을 고를 확률은 1/6(표준화하여 1/3)이 됩니다. 반대로 선택을 변경하면 확률은 1/3(표준화하여 2/3)이 됩니다. 선택을 변경하는 것이 자동차를 선택할 확률이 더 높습니다.
Monty Hall 풀이2: LOTP(Law of Total Probability)
마찬가지로 참가자는 어떤 문 뒤에 자동차가 있는지 알기 원합니다. S는 참가자가 자동차가 있는 문을 선택하는 경우를 의미하며 Monty의 물음에 따라 항상 선택한 문을 변경한다고 가정합니다. $D_{j}, j \in 1,2,3$는 자동차가 존재하는 문 번호입니다. $P(S)$는 아래와 같이 계산할 수 있습니다.
$P(S) = P(S \mid D_{1})\frac{1}{3} + P(S \mid D_{2})\frac{1}{3} + P(S \mid D_{3})\frac{1}{3}$
자동차가 1번 문에 있다고 가정하면,
$= 0 + 1\frac{1}{3} + 1\frac{1}{3} = \frac{2}{3}$
Simpson’s Paradox
일부 부분에서 성립하는 대소관계는 전체로 보았을 때 역전될 수 있다는 역설입니다.
심슨 가족이 사는 스프링필드에 Dr.Hibbert와 Dr.Nick 두 명의 의사가 있습니다. 이들은 심장수술과 반창고 시술 두 가지 서비스를 제공합니다. 100번을 시도했을 때 성공, 실패 횟수는 아래와 같습니다.
## IMO *** Monty hall 문제는 볼 때마다 헷갈렸는데 수형도를 통해 푸는 방법을 잘 기억해 두어야 겠습니다. Simpson's paradox의 개념도 잘 알아 두어야 겠습니다.