ch7. Gambler's Ruin and Random Variables

Intro

Gambler’s Ruin 문제를 계차방정식을 이용해 풀고, 확률변수의 정의를 이해할 수 있습니다.

A, B 두 명의 gambler가 내기를 합니다. 매 round에서 1 dollar를 걸고 내기에서 이긴 사람이 가져갑니다. A는 i dollar, B는 (N-i) dollar를 가지고 시작합니다.

p = A가 이길 확률

q = B가 이길 확률 = 1-p

위 문제는 유형을 파악하는 것이 중요합니다. 이와 같은 유형의 문제는 random walk로 정의할 수 있습니다.

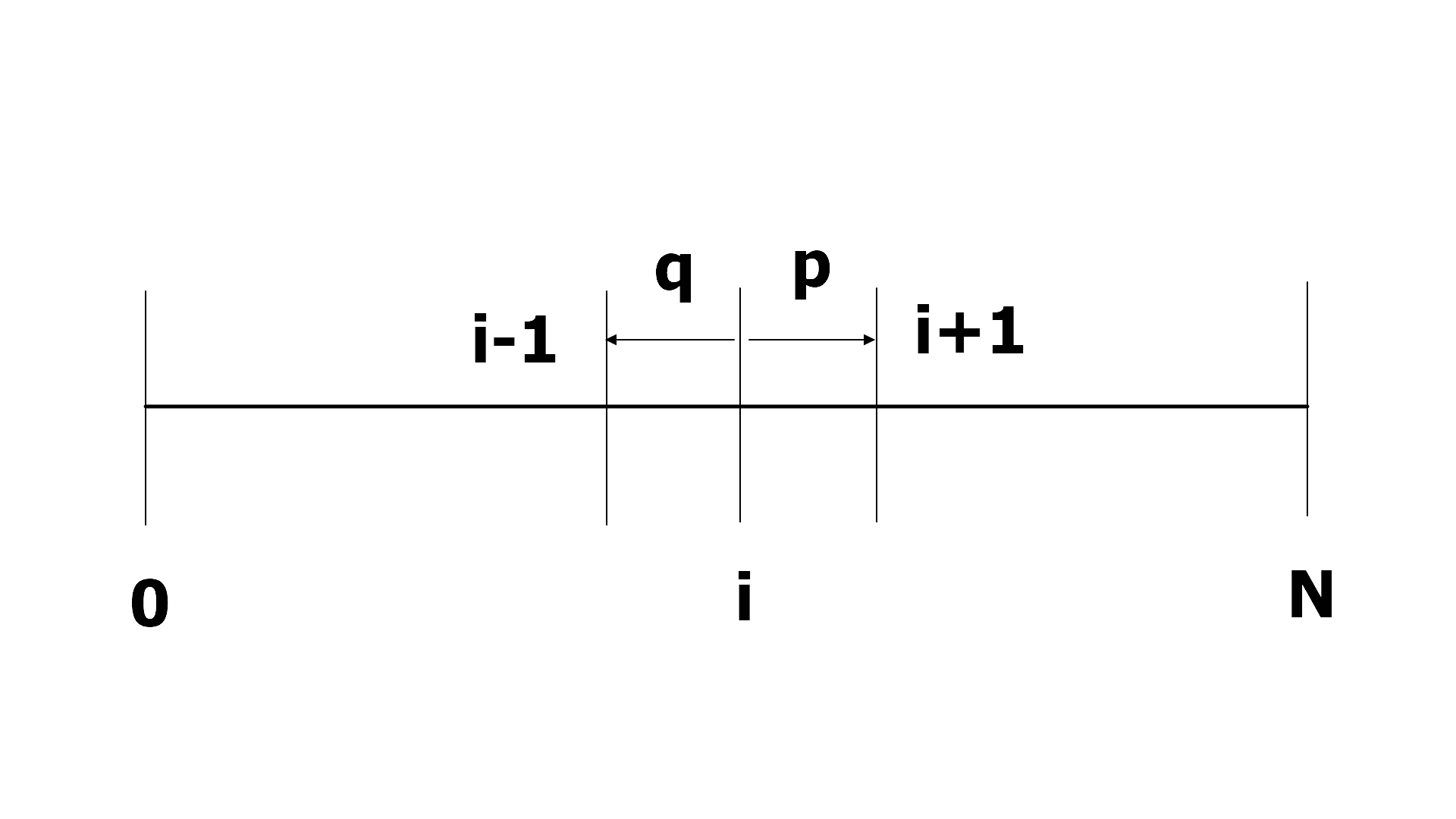
Post-Image

p는 오른쪽으로 이동할 확률, q는 왼쪽으로 이동할 확률입니다. 0, N은 absorbing state로 갇힌 상태입니다.

Strategy: Condition on first step

$P_{i} = P(A wins game \mid A starts at i dollar)$

$P_{i} = pP_{i+1} + qP_{i-1}$, $(1 \leq i \leq N-1)$, $(p_{0}=0, p_{N}=1)$

문제를 해결하는데 가장 중요한 식입니다. Difference qeuation(계차방정식)이라고 부르며 미분방정식의 이산 형태입니다.

Guessing을 통한 풀이

$P_{i} = x^{i}$

$x^{i} = px^{i+1} + qx^{i-1}$

$px^{2} - x + q = 0$

$x = \frac{1 \pm \sqrt{1 - 4pq}}{2p} \in {1,\frac{q}{p}}$

두 해가 다른 경우($p \neq q$)
두 해의 선형결합 식으로 표현할 수 있습니다.
$p_{i} = A1^{i} + B(\frac{q}{p})^{i}, (p \neq q)$
조건 $p_{0} = 0, p_{N} = 1$을 대입하면,
$p_{0} = A + B = 0$$, B = -A$
$p_{N} = A + B(\frac{q}{p})^{N} = A(1 - (\frac{q}{p})^{N}) = 1$
$A = \frac{1}{1 - (\frac{q}{p})^{N}}$
$p_{i} = \frac{1 - (\frac{q}{p})^{i}}{1 - (\frac{q}{p})^{N-1}}, (p \neq q)$
두 해가 같은 경우($p = q$)
$x = \frac{q}{p}$로 치환하고 $x \to 1$의 극한을 살펴봅니다.
$\lim_{x \to 1} \frac{1-x^{i}}{1-x^{N}} = \lim_{x \to 1} \frac{i(x^{i-1})}{N(x^{N-1})} = \frac{i}{N}$

카지노(A)와 gambler(B)가 같은 돈을 가지고 시작했을 때 카지노에게 1%라도 유리한 게임인 경우 gambler가 이길 확률은 매우 작아집니다.

$i = N-i, p=0.49$
$N=20 \to 0.40$
$N=100 \to 0.12$
$N=200 \to 0.02$

우선 확률변수의 정의를 알아봅시다. 확률변수는 function입니다. 이 function은 표본공간 S로부터 실수 체계 R로 mapping합니다.

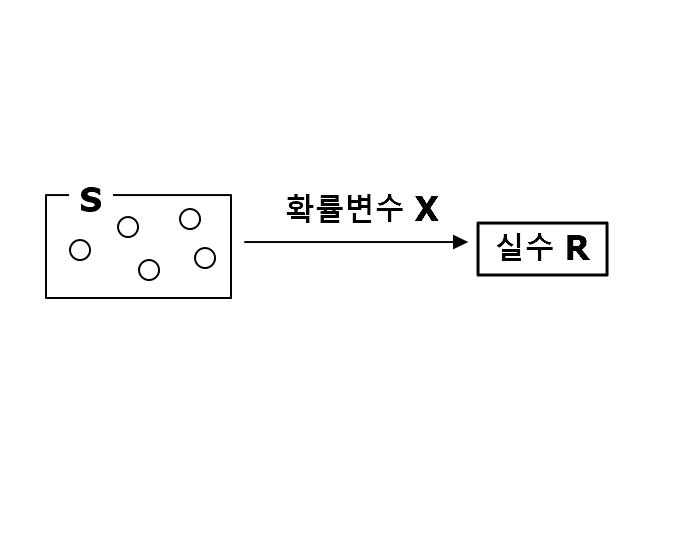
Post-Image

쉽고 중요한 예제들을 살펴봅니다.

Bernoulli (베르누이) 확률분포
A random variable X is said to have Bernoulli(p) distribution, if X has only 2 possible values, 0 and 1
P(X=1) = p
P(X=0) = 1-P
Binomial (이항) 확률분포 (n,p)
The distribution of #success X in n independent Bernoulli(p) trials is called Binomial(n,p), its distribution is given by
$P(X=k) = \binom{n}{k} p^{k}(1-p)^{n-k}$
이 식은 PMF(확률질량변수)라고 합니다.
X~Bin(n,p), Y~Bin(m,p), X와 Y가 independent일 때 X+Y~Bin(n+m, p)를 따릅니다.

Difference equation(계차방정식)을 다루는 곳이 거의 없는데 중요한 개념으로 보입니다. 베르누이분포, 이항분포를 시작으로 확률변수 분포가 나오는데 잘 정리해야 겠습니다.